已知函数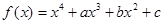 ,在
,在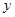 轴上的截距为
轴上的截距为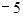 ,在区间
,在区间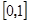 上单调递增,在
上单调递增,在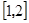 上单调递减,又当
上单调递减,又当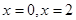 时取得极小值.
时取得极小值.
(1)求函数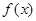 的解析式;
的解析式;
(2)能否找到函数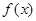 垂直于
垂直于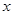 轴的对称轴,并证明你的结论;
轴的对称轴,并证明你的结论;
(3)设使关于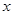 的方程
的方程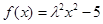 恰有三个不同实根的实数
恰有三个不同实根的实数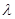 的取值范围为集合
的取值范围为集合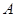 ,且两个非零实根为
,且两个非零实根为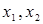 ,试问:是否存在实数
,试问:是否存在实数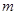 ,使得不等式
,使得不等式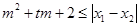 对任意
对任意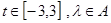 恒成立?若存在,求
恒成立?若存在,求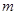 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
假设每一架飞机的引擎在飞行中出现故障的概率为1-P,且各引擎是否出故障是独立的,已知4引擎飞机中至少有3个引擎正常运行,飞机就能成功运行;2引擎飞机中要2个引擎全部正常运行,飞机才能成功运行.要使4引擎飞机比2引擎飞机更安全,则P的取值范围?
有10道单项选择题,每题有4个选项。某人随机选其中一个答案(每个选项被选出的可能性相同),求答对多少题的概率最大?并求出此种情况下概率的大小.(保留两位有效数字)
在一次抗洪抢险中,,准备用射击的方法引爆从桥上游漂流而下的一个巨大的汽油灌,已知只有5发子弹,第一次命中只能使汽油流出,第二次命中才能引爆。每次射击相互独立,且命中概率都是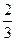 ,求(1)油罐被引爆的概率;
,求(1)油罐被引爆的概率;
(2)如果引爆或子弹打光则停止射击,设射击次数为ξ,求ξ的分布列.
袋中有4个红球,2个白球,一次摸出一球然后放回,共摸三次.记Y为摸出的三个球中白球的个数,求Y的分布列.
在对人们休闲的一次调查中,共调查了124人,其中女性70人,男性54人.女性中有43人主要的休闲方式是看电视,另外27人的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(1)根据以上数据建立一个2×2的列联表;
(2)画出三维柱形图和二维条形图;
(3)检验性别是否与休闲方式有关,可靠性有多大.