已知曲线 和
和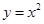 相交于点A,
相交于点A,
(1)求A点坐标;
(2)分别求它们在A点处的切线方程(写成直线的一般式方程);
(3)求由曲线 在A点处的切线及
在A点处的切线及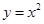 以及
以及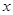 轴所围成的图形面积。(画出草图)
轴所围成的图形面积。(画出草图)
(本小题满分8分)
已知函数
(1) 若函数 的图象经过点
的图象经过点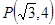 ,求
,求 的值;
的值;
(2) 判断并证明函数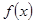 的奇偶性;
的奇偶性;
(3) 比较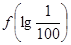 与
与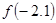 的大小,并写出必要的理由.
的大小,并写出必要的理由.
(本小题满分8分)
已知全集 ,
,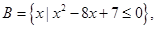
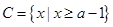
(1)求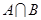 ;
; 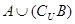
(2)若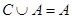 ,求实数
,求实数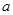 的取值范围.
的取值范围.
已知点 的坐标为
的坐标为 ,点
,点 在圆
在圆 上运动,以点
上运动,以点 为一端点作线段
为一端点作线段 ,使得点
,使得点 为线段
为线段 的中点.
的中点.
(1)求线段 端点
端点 轨迹
轨迹 的方程;
的方程;
(2)已知直线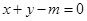 与轨迹
与轨迹 相交于两点
相交于两点 ,以
,以 为直径的圆经过坐标原点
为直径的圆经过坐标原点 ,求实数
,求实数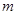 的值
的值
如图,三棱柱 中,侧棱
中,侧棱 ,且侧棱和底面边长均为2,
,且侧棱和底面边长均为2,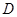 是
是 的中点
的中点
(1)求证: ;
;
(2)求证: ;
;
(3)求三棱锥 的体积
的体积
已知圆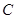 与
与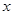 轴相切,圆心
轴相切,圆心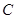 在射线
在射线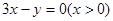 上,直线
上,直线 被圆
被圆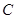 截得的弦长为2
截得的弦长为2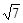

(1)求圆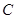 标准方程;
标准方程;
(2)已知点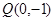 ,经过点
,经过点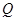 直线
直线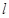 与圆
与圆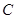 相切于
相切于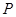 点,求
点,求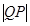 的值.
的值.