已知定义在正实数集上的函数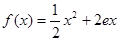 ,
,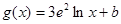 (其中
(其中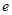 为常数,
为常数,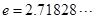 ),若这两个函数的图象有公共点,且在该点处的切线相同。
),若这两个函数的图象有公共点,且在该点处的切线相同。
(Ⅰ)求实数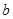 的值;
的值;
(Ⅱ)当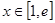 时,
时, 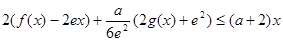 恒成立,求实数
恒成立,求实数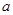 的取值范围.
的取值范围.
对于三次函数 ,定义
,定义 是
是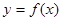 的导函数
的导函数 的导函数,若方程
的导函数,若方程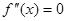 有实数解
有实数解 ,则称点
,则称点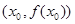 为函数
为函数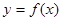 的“拐点”,可以证明,任何三次函数都有“拐点”,任何三次函数都有对称中心,且“拐点”就是对称中心,请你根据这一结论判断下列命题:
的“拐点”,可以证明,任何三次函数都有“拐点”,任何三次函数都有对称中心,且“拐点”就是对称中心,请你根据这一结论判断下列命题:
①任意三次函数 都关于点
都关于点 对称:
对称:
②存在三次函数 ,若
,若 有实数解
有实数解 ,则点
,则点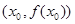 为函数
为函数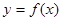 的对称中心;
的对称中心;
③存在三次函数有两个及两个以上的对称中心;
④若函数 ,则:
,则: 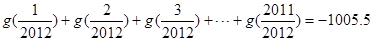
其中所有正确结论的序号是().
| A.①②④ | B.①②③ | C.①③④ | D.②③④ |
已知向量 =(sin(
=(sin( +x),
+x), cosx),
cosx), ="(sinx,cosx)," f(x)=
="(sinx,cosx)," f(x)=  ·
· .
.
(1)求f(x)的最小正周期和单调增区间;
(2)如果三角形ABC中,满足f(A)= ,求角A的值.
,求角A的值.
如图,在四棱锥P-ABCD中,底面ABCD是∠DAB=60°,且边长为a的菱形,侧面PAD为正三角形,其所在平面垂直底面ABCD.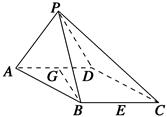
(1)若G为AD边的中点,求证:BG⊥平面PAD;
(2)求证:AD⊥PB;
(3)若E为BC边的中点,能否在棱PC上找到一点F,使平面DEF⊥平面ABCD,并证明你的结论.
已知函数 处取得极小值-4,使其导函数
处取得极小值-4,使其导函数 的取值范围为(1,3)。
的取值范围为(1,3)。
(1)求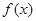 的解析式及
的解析式及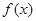 的极大值;
的极大值;
(2)当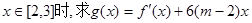 的最大值。
的最大值。
已知函数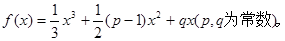
(1)若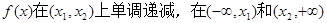 上单调递增,且
上单调递增,且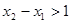 ,求证:
,求证: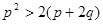
(2)若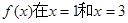 处取得极值,且在
处取得极值,且在 时,函数
时,函数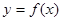 的图象在直线
的图象在直线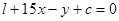 的下方,求c的取值范围.
的下方,求c的取值范围.