在海岸A处,发现北偏东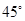 方向,距离A为
方向,距离A为 海里的B处有一走私船,在A北偏西
海里的B处有一走私船,在A北偏西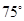 方向距离A为2海里的C处有我方一艘缉私艇奉命以
方向距离A为2海里的C处有我方一艘缉私艇奉命以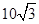 海里/小时的速度追截走私船,且C在B的正西方,此时走私船正以
海里/小时的速度追截走私船,且C在B的正西方,此时走私船正以 海里/小时的速度从B处向北偏东
海里/小时的速度从B处向北偏东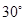 方向逃窜,问缉私艇沿什么方向,才能最快追上走私船?需要多长时间?
方向逃窜,问缉私艇沿什么方向,才能最快追上走私船?需要多长时间?
(本小题满分13分)
已知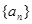 是单调递增的等差数列,首项
是单调递增的等差数列,首项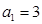 ,前
,前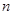 项和为
项和为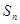 ,数列
,数列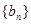 是等比数列,首项
是等比数列,首项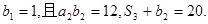 (Ⅰ)求
(Ⅰ)求 的通项公式。
的通项公式。
(Ⅱ)令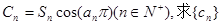 的前n项和
的前n项和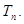
(本小题满分12分)已知椭圆的焦点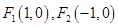 ,过
,过 作垂直于
作垂直于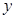 轴的直线被椭圆所截线段长为
轴的直线被椭圆所截线段长为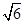 ,过
,过 作直线l与椭圆交于A、B两点.(I)求椭圆的标准方程;(Ⅱ)是否存在实数
作直线l与椭圆交于A、B两点.(I)求椭圆的标准方程;(Ⅱ)是否存在实数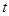 使
使 ,若存在,求
,若存在,求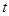 的值和直线
的值和直线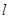 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
(本小题满分12分).
如图是某直三棱柱被削去上底后所得几何体的直观图、左视图、俯视图,在直观图中,M是
BD的中点,左视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示。
(Ⅰ)求该几何体的体积;(Ⅱ)求证:EM∥平面ABC;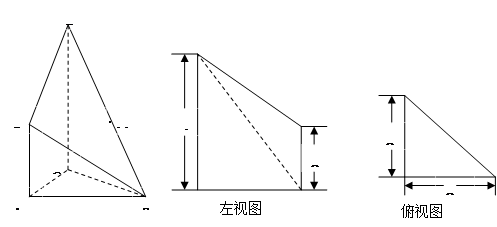
(本小题满分12分)
某日用品按行业质量标准分成五个等级,等级系数X依次为1,2,3,4,5.现从一批该日用
品中随机抽取20件,对其等级系数进行统计分析,得到频率分布表如下:
| X |
1 |
2 |
3 |
4 |
5 |
| 频率 |
a |
0.2 |
0.4 |
b |
c |
(I)若所抽取的20件日用品中,等级系数为4的恰有3件,等级系数为5的恰有2件,
求a,b,c的值;
(Ⅱ)在(I)的条件下,将等级系数为4的3件日用品记为x1,x2,x3,等级系数为5的2件
日用品记为y1,y2,现从x1,x2,x3,y1,y2这5件日用品中任取两件(假定每件日用品被取出
的可能性相同),写出所有可能的结果,并求这两件日用品的等级系数恰好相等的概率
(本小题满分12分)
在 中,
中, .
.
(I)求角 的大小;
的大小;
(II)若 ,
,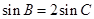 ,求
,求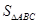 .
.