某学校要建造一个面积为10000平方米的运动场.如图，运动场是由一个矩形ABCD和分别以AD、BC为直径的两个半圆组成.跑道是一条宽8米的塑胶跑道，运动场除跑道外，其他地方均铺设草皮.已知塑胶跑道每平方米造价为150元，草皮每平方米造价为30元
（1）设半圆的半径OA=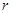
(米),试建立塑胶跑道面积S与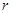的函数关系S(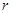) ，并求其定义域；
（2）由于条件限制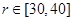
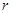,问当取何值时,运动场造价最低?（
取3.14）
设双曲线C：
－y2＝1的左、右顶点分别为A1、A2，垂直于x轴的直线m与双曲线C交于不同的两点P、Q．
（1）若直线m与x轴正半轴的交点为T，且
·
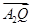＝1，求点T的坐标；
（2）求直线A1P与直线A2Q的交点M的轨迹E的方程；
（3）过点F（1，0）作直线l与（2）中的轨迹E交于不同的两点A、B，设
＝λ·
，若λ∈[－2，－1]，求|
＋
|（T为（1）中的点）的取值范围．
已知函数f(x)＝2x－
－aln(x＋1)，a∈R．
（1）若a＝－4，求函数f(x)的单调区间；
（2）求y＝f(x)的极值点（即函数取到极值时点的横坐标）．
已知数列{an}为等差数列，它的前n项和为Sn，且a3＝5，S6＝36 ．
（1）求数列{an}的通项公式；
（2）数列{bn}满足bn＝(－3)n·an，求数列{bn}的前n项和Tn．
有一种摸奖游戏，一个不透明的袋中装有大小相同的红球5个，白球10个，摸奖者每次随机地从袋中摸出5个球查看后再全部放回，若这5个球中有3个红球则中三等奖，有4个红球则中二等奖，有5个红球则中一等奖．
（1）某人摸奖一次，问他中奖的概率有多大？
（2）某人摸奖一次，若已知他中奖了，问他中二等奖的概率有多大？
如图，在直三棱柱ABC－A1B1C1中，AC＝BC＝2，AA1＝2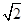
，∠ACB＝900，M是AA1的中点，N是BC1的中点．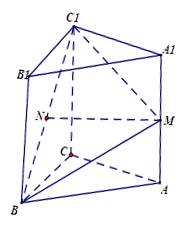
（1）求证：MN//平面A1B1C1；
（2）求二面角B－C1M－C的平面角余弦值的大小．