如图,在四棱锥P—ABCD中,底面ABCD是边长为4的菱形,且 ,菱形ABCD的两条对角线的交点为0,PA=PC,PB=PD,且PO=3.点E是线段PA的中点,连接EO、EB、EC.
,菱形ABCD的两条对角线的交点为0,PA=PC,PB=PD,且PO=3.点E是线段PA的中点,连接EO、EB、EC.
(I)证明:直线OE//平面PBC;
(II)求二面角E-BC-D的大小
(理科)已知椭圆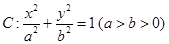 经过点
经过点 ,离心率为
,离心率为 .(Ⅰ)求椭圆
.(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)直线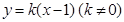 与椭圆
与椭圆 交于
交于 两点,点
两点,点 是椭圆
是椭圆 的右顶点.直线
的右顶点.直线 与直线
与直线 分别与
分别与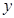 轴交于点
轴交于点 ,试问以线段
,试问以线段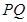 为直径的圆是否过
为直径的圆是否过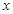 轴上的定点?若是,求出定点坐标;若不是,说明理由.
轴上的定点?若是,求出定点坐标;若不是,说明理由.
(文科)已知椭圆
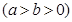 的右焦点为
的右焦点为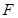
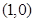 ,短轴的端点分别为
,短轴的端点分别为 ,且
,且 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)过点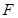 且斜率为
且斜率为
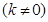 的直线
的直线 交椭圆于
交椭圆于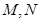 两点,弦
两点,弦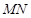 的垂直平分线与
的垂直平分线与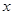 轴相交于点
轴相交于点 .设弦
.设弦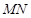 的中点为
的中点为 ,试求
,试求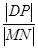 的取值范围.
的取值范围.
(理科)已知双曲线 的离心率为
的离心率为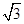 ,右准线方程为
,右准线方程为
(Ⅰ)求双曲线 的方程;
的方程;
(Ⅱ)设直线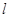 是圆
是圆 上动点
上动点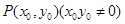 处的切线,
处的切线,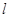 与双曲线
与双曲线 交于不同的两点
交于不同的两点 ,证明
,证明 的大小为定值.
的大小为定值.
(文科)已知椭圆 (
( )的四个顶点恰好是一边长为
)的四个顶点恰好是一边长为 ,一内角为
,一内角为 的菱形的四个顶点.
的菱形的四个顶点.
(1)求椭圆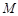 的方程;
的方程;
(2)直线 与椭圆
与椭圆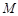 交于
交于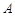 ,
,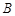 两点,且线段
两点,且线段 的垂直平分线经过点
的垂直平分线经过点 ,求
,求 (
(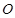 为原点)面积的最大值.
为原点)面积的最大值.
(理科)已知椭圆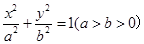 的离心率
的离心率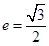 ,连接椭圆的四个顶点得到的菱形的面积为4。
,连接椭圆的四个顶点得到的菱形的面积为4。
(1)求椭圆的方程;
(2)设直线 与椭圆相交于不同的两点
与椭圆相交于不同的两点 ,已知点
,已知点 的坐标为(
的坐标为(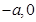 ),点
),点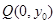 在线段
在线段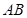 的垂直平分线上,且
的垂直平分线上,且 ,求
,求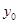 的值
的值