巳知数列{an}的前n项和为
，且
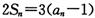，数列{bn}满足
，
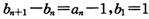(I)证明：数列{an}为等比数列；
(II)求数列{an}和{bn}的通项公式；
(III)记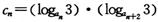
，数列{cn}的前n项和为Tn，比较2Tn与
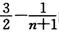的大小.
已知函数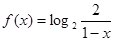
．
（Ⅰ）求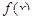
的定义域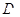
及其零点；
（Ⅱ）判断函数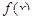在定义域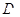上的单调性，并用函数单调性定义证明．
（Ⅰ）求值：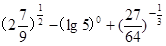
（Ⅱ）求值：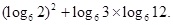
已知定义域为R的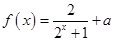函数
是奇函数，
（1）求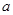
的值．
（2）判断函数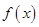
在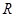
上的单调性并加以证明；
（3）若对于任意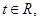
不等式
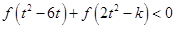恒成立，求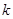
的取值范围．
已知函数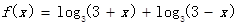
．
（1）求函数f（x）的定义域和值域；
（2）判断函数f（x）的奇偶性，并说明理由．
邵东某桶装水经营部每天的房租、人员工资等固定成本为360元，每桶水进价4元，销售单价与日均销量的关系如表所示
| 销售单价/元 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
| 日均销售量/桶 |
360 |
320 |
280 |
240 |
200 |
160 |
120 |
请根据以上数据作出分析，这个经营部怎样定价（单价要为整元）才能获得最大利润？最大利润为多少？