用起重机把质量为2.0×103kg的物体匀速地提高9m。重力加速度g取10m/s2。试求:(1)钢绳的拉力做了多少功?
(2)重力做了多少功?
(3)若钢绳拉力改为2.4×104N,起重机把物体由静止开始匀加速提高9m,则在此过程中钢绳拉力做功的功率为多少?
两个完全相同的小球甲、乙,当甲由某高度由静止释放的同时,小球乙由地面以20m/s的速度竖直向上抛出,相遇时甲、乙两球通过的位移大小正好相等。不计空气的阻力,重力加速度取g=10m/s2求:
(1)甲、乙两小球从开始到相遇的时间;
(2)甲球释放点到地面的高度。
(3)通过计算说明甲乙谁先落地;
一质点由A点由静止出发沿直线AB运动,先作加速度大小为a1的匀加速直线运动,紧接着作加速度大小为a2的匀减速直线运动,抵达B点时恰好静止。如果AB的总长度是S,试求
(1)运动过程中的最大速度;
(2) 质点走完AB所用的时间t.
(9分)如图所示,一个人用与水平方向成 角的斜向下的推力
角的斜向下的推力 推一个重
推一个重 的箱子匀速前进,箱子与地面间的动摩擦因数为
的箱子匀速前进,箱子与地面间的动摩擦因数为 (
(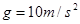 )。求:
)。求: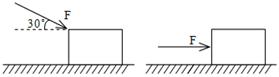
(1)推力 的大小;
的大小;
(2)若人不改变推力 的大小,只把力的方向变为水平去推这个静止的箱子,推力作用时间
的大小,只把力的方向变为水平去推这个静止的箱子,推力作用时间 后撤去,箱子最远运动多长距离.
后撤去,箱子最远运动多长距离.
可视为质点的小球A、B静止在光滑水平轨道上,A的左边固定有轻质弹簧,B与弹簧左端接触但不拴接,A的右边有一垂直于水平轨道的固定挡板P。左边有一小球C沿轨道以某一初速度射向B球,如图所示,C与B发生碰撞并立即结成一整体D,在它们继续向右运动的过程中,当 D和A的速度刚好相等时,小球A恰好与挡板P发生碰撞,碰后A立即静止并与挡板P粘连。之后D被弹簧向左弹出,D冲上左侧与水平轨道相切的竖直半圆光滑轨道,其半径为 ,D到达最高点Q时,D与轨道间弹力
,D到达最高点Q时,D与轨道间弹力 。已知三小球的质量分别为
。已知三小球的质量分别为 、
、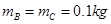 。取
。取 ,求:
,求: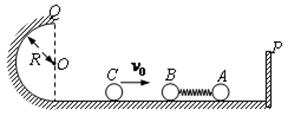
(1)D到达最高点Q时的速度 的大小;
的大小;
(2)D由Q点水平飞出后的落地点与Q点的水平距离s;
(3)C球的初速度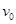 的大小。
的大小。
如图所示,轻杆两端分别系着质量为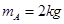 的圆环A和质量为
的圆环A和质量为 的小球B,轻杆与A的连接处有光滑铰链,轻杆可以绕铰链自由转动。A套在光滑的水平固定横杆上,A、B静止不动时B球恰好与光滑地面接触,在B的左侧是半径为
的小球B,轻杆与A的连接处有光滑铰链,轻杆可以绕铰链自由转动。A套在光滑的水平固定横杆上,A、B静止不动时B球恰好与光滑地面接触,在B的左侧是半径为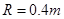 m的1/4圆弧。质量为
m的1/4圆弧。质量为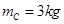 的小球C以
的小球C以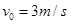 的速度向左与B球发生正碰。已知碰后C小球恰好能做平抛运动,小球B在运动过程中恰好能与横杆接触。重力加速度取
的速度向左与B球发生正碰。已知碰后C小球恰好能做平抛运动,小球B在运动过程中恰好能与横杆接触。重力加速度取 ,则:
,则: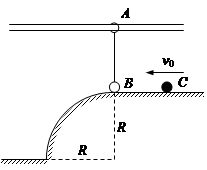
(1)碰后C球平抛的水平位移(2)碰后瞬间B球的速度(3)A、B间轻杆的长度