阅读下列材料:
正方形网格中,每个小正方形的顶点称为格点.以格点为顶点的多边形叫格点多边形,若格点多边形至少有一边是曲线,则称其为曲边格点多边形.
(1)求图(1)中格点三角形的面积;
(2)在图(2)中画出一个格点梯形,使它的面积等于9;(只需画出,不必说明)
(3)在图(3)中画出一个曲边格点多边形,使它的面积等于25,说明理由.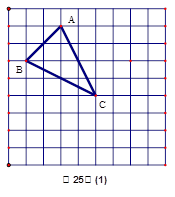
某同学在学习了正多边形和圆之后,对正五边形的边及相关线段进行研究,发现多处出现著名的黄金分割比 .如图,圆内接正五边形 ,圆心为 , 与 交于点 , 、 与 分别交于点 、 .根据圆与正五边形的对称性,只对部分图形进行研究.(其它可同理得出)
(1)求证: 是等腰三角形且底角等于 ,并直接说出 的形状;
(2)求证: ,且其比值 ;
(3)由对称性知 ,由(1)(2)可知 也是一个黄金分割数,据此求 的值.

"通过等价变换,化陌生为熟悉,化未知为已知"是数学学习中解决问题的基本思维方式,例如:解方程 ,就可以利用该思维方式,设 ,将原方程转化为: 这个熟悉的关于 的一元二次方程,解出 ,再求 ,这种方法又叫"换元法".请你用这种思维方式和换元法解决下面的问题.
已知实数 , 满足 ,求 的值.
为了发展学生的健康情感,学校开展多项体育活动比赛,促进学生加强体育锻炼,注重增强体质,从全校2100名学生60秒跳绳比赛成绩中,随机抽取60名同学的成绩,通过分组整理数据得到下面的样本频数分布表.
|
跳绳的次数 |
频数 |
|
|
4 |
|
|
6 |
|
|
11 |
|
|
22 |
|
|
10 |
|
|
4 |
|
|
(1)已知样本中最小的数是60,最大的数是198,组距是20,请你将该表左侧的每组数据补充完整;
(2)估计全校学生60秒跳绳成绩能达到最好一组成绩的人数;
(3)若以各组组中值代表各组的实际数据,求出样本平均数(结果保留整数)及众数;分别写出用样本平均数和众数估计全校学生60秒跳绳成绩得到的推断性结论.
已知自变量 与因变量 的对应关系如表呈现的规律.
|
|
|
|
|
0 |
1 |
2 |
|
|
|
|
12 |
11 |
10 |
9 |
8 |
|
(1)直接写出函数解析式及其图象与 轴和 轴的交点 , 的坐标;
(2)设反比例函数 的图象与(1)求得的函数的图象交于 , 两点, 为坐标原点且 ,求反比例函数解析式;已知 ,点 与 分别在反比例函数与(1)求得的函数的图象上,直接写出 与 的大小关系.
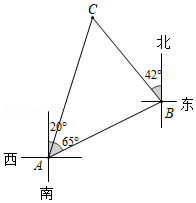
如图,一艘船由 港沿北偏东 方向航行 到 港,然后再沿北偏西 方向航行至 港,已知 港在 港北偏东 方向.
(1)直接写出 的度数;
(2)求 、 两港之间的距离.(结果用含非特殊角的三角函数及根式表示即可)