如图，已知：△ABC为边长是
的等边三角形，四边形DEFG为边长是6的正方形.现将等边△ABC和正方形DEFG按如图1的方式摆放，使点C与点E重合，点B、C（E）、F在同一条直线上，△ABC从图1的位置出发，以每秒1个单位长度的速度沿EF方向向右匀速运动，当点C与点F重合时暂停运动，设△ABC的运动时间为t秒(
).
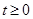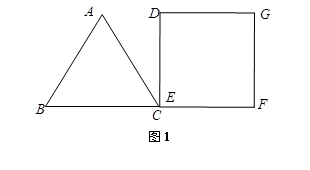
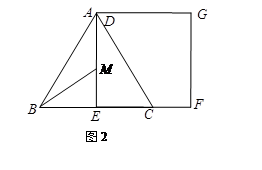
在整个运动过程中，设等边△ABC和正方形DEFG重叠部分的面积为S，请直接写出S与t之间的函数关系式；
如图2，当点A与点D重合时，作
的角平分线EM交AE于M点，将△ABM绕点A逆时针旋转，使边AB与边AC重合，得到△ACN.在线段AG上是否存在H点，使得△ANH为等腰三角形.如果存在，请求出线段EH的长度；若不存在，请说明理由.如图3，若四边形DEFG为边长为
的正方形，△ABC的移动速度为每秒
个单位长度，其余条件保持不变.△ABC开始移动的同时，Q点从F点开始，沿折线FG-GD以每秒
个单位长度开始移动，△ABC停止运动时，Q点也停止运动.设在运动过程中，DE交折线BA-AC于P点，则是否存在t的值，使得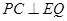
，若存在，请求出t的值；若不存在，请说明理由
如图，正方形网格中的每个小正方形的边长都是1，顶点叫做格点．△ABC的三个顶点A，B，C都在格点上．将△ABC绕点A按顺时针方向旋转90°得到△AB′C′．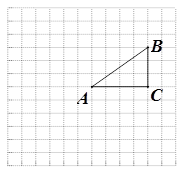
（1）在正方形网格中，画出△AB′C′；
（2）计算线段AB在变换到AB′的过程中扫过的区域的面积．
如图，在平面直角坐标系中，以点C（1，1）为圆心，2为半径作圆，交
轴
于
两点，点
在⊙
上．
（1）求出两点的坐标；
（2）试确定经过A、B且以点P为顶点的抛物线解析式；
（3）在该抛物线上是否存在一点
，使线段
与
互相平分？若存在，求出点的坐标；若不存在，请说明理由．
如图，点C在以AB为直径的半圆上，AB=8，∠CBA=30°，点D在线段AB上从点A运动到点B，点E与点D关于AC对称，DF⊥DE于点D，并交EC的延长线于点F.
（1）求证：CE=CF；
（2）求线段EF的最小值；
（3）当点D从点A运动到点B时，线段EF扫过的面积的大小是 ．
已知:如图，二次函数y=a（x﹣h）2+
的图象经过原点O（0，0），A（2，0）．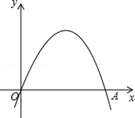
（1）写出该函数图象的对称轴；
（2）若将线段OA绕点O逆时针旋转60°到OA′，试判断点A′是否为该函数图象的顶点？请说明理由.
已知：如图1，在面积为3的正方形ABCD中，E、F分别是BC和CD边上的两点，AE⊥BF于点G，且BE=1．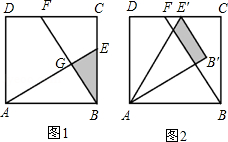
（1）求出△ABE和△BCF重叠部分（即△BEG）的面积；
（2）现将△ABE绕点A逆时针方向旋转到△AB′E′（如图2），使点E落在CD边上的点E′处，问△ABE在旋转前后与△BCF重叠部分的面积是否发生了变化？请说明理由．