如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连结BF。BD与CD有什么数量关系,并说明理由;
当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由。

如图1,若四边形ABCD、四边形CFED都是正方形,显然图中有AG=CE,AG⊥CE.当正方形GFED绕D旋转到如图2的位置时,AG=CE, AG⊥CH是否成立?若成立,请给出证明;若不成立,请说明理由.
当正方形GFED绕D旋转到如图3的位置时,延长CE交AG于H,交AD于M.当AD=4,DG=
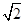 时,求CH的长。
时,求CH的长。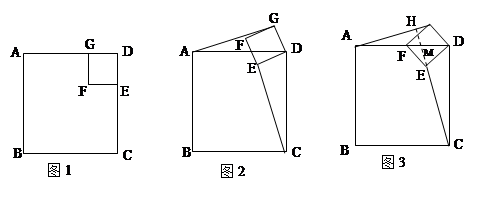
如图,AB为⊙O的直径,AD平分∠BAC交⊙O于点D,DE⊥AC交AC的延长线于点E,FB是⊙O的切线交AD的延长线于点F.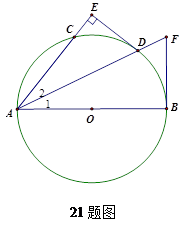
求证:DE是⊙O的切线
若DE=3,⊙O的半径为5,求BF的长
已知反比例函数y=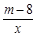 (m为常数)的图象经过点A(-1,6)
(m为常数)的图象经过点A(-1,6) .
.求m的值
如图,过点A作直线AC与函数y=
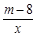 的图象交于点B,与x轴交于点C,且AB=2BC,求点C的坐标
的图象交于点B,与x轴交于点C,且AB=2BC,求点C的坐标
如图,在网格中、建立了平面直角坐标系,每个小正方形的边长均为1个单位长度,将四边形ABCD绕坐标原点O按顺时针方向旋转180°后得到四边形A1B1C1D1.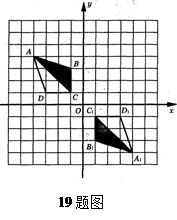
写出点D1的坐标_________,点D旋转到点D1所经过的路线长__________;
请你在△ACD的三个内角中任选二个锐角,若你所选的锐角是________,则它所对应的正弦函数值是_________
将四边形A1B1C1D1平移,得到四边形A2B2C2D2,若点D2 (4,5),画出平移后的图形.
某公司组织部分员工到一博览会的A、B、C、D、E五个展馆参观,公司所购门票种类、数量绘制成的条形和扇形统计图如图所示.

请根据统计图回答下列问题:B馆门票多少张?C馆门票占所购门票的比例是多少?
若
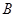 馆门票仅剩下一张,而员工小明和小华都想要,他们决定采用抽扑克牌的
馆门票仅剩下一张,而员工小明和小华都想要,他们决定采用抽扑克牌的
方法来确定,规则是:“将同一副牌中正面分别标有数字1,2,3,4的四张牌洗匀
后,背面朝上放置在桌面上,每人随机抽一次且一次只抽一张;一人抽后记下数字,
将牌放回洗匀背面朝上放置在桌面上,再由另一人抽.若抽出的两次数字之积为偶
数则小明获得门票,反之小华获得门票.” 请用画树状图或列表的方法计算出小明和
小华获得门票的概率,并说明这个规则对双方是否公平.