如图1,若四边形ABCD、四边形CFED都是正方形,显然图中有AG=CE,AG⊥CE.当正方形GFED绕D旋转到如图2的位置时,AG=CE, AG⊥CH是否成立?若成立,请给出证明;若不成立,请说明理由.
当正方形GFED绕D旋转到如图3的位置时,延长CE交AG于H,交AD于M.当AD=4,DG=
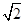 时,求CH的长。
时,求CH的长。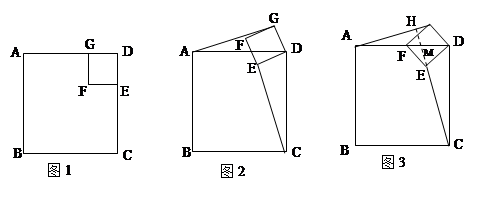
已知:平面直角坐标系中,四边形OABC的顶点分别为O(0,0)、A(5,0)、B(m,2)、C(m-5,2).
(1)问:是否存在这样的m,使得在边BC上总存在点P,使∠OPA=90º?若存在,求出m的取值范围;若不存在,请说明理由.
(2)当∠AOC与∠OAB的平分线的交点Q在边BC上时,求m的值.
某工厂以80元/箱的价格购进60箱原材料,准备由甲、乙两车间全部用于生产A产品.甲车间用每箱原材料可生产出A产品12千克,需耗水4吨;乙车间通过节能改造,用每箱原材料可生产出的A产品比甲车间少2千克,但耗水量是甲车间的一半.已知A产品售价为30元/千克,水价为5元/吨.如果要求这两车间生产这批产品的总耗水量不得超过200吨,那么该厂如何分配两车间的生产任务,才能使这次生产所能获取的利润w最大?最大利润是多少?(注:利润=产品总售价-购买原材料成本-水费)
(1)甲、乙、丙、丁四人做传球游戏:第一次由甲将球随机传给乙、丙、丁中的某一人,从第二次起,每一次都由持球者将球再随机传给其他三人中的某一人.求第二次传球后球回到甲手里的概率.(请用“画树状图”或“列表”等方式给出分析过程)
(2)如果甲跟另外n(n≥2)个人做(1)中同样的游戏,那么,第三次传球后球回到甲手里的概率是(请直接写出结果).
某区教研部门对本区初二年级的学生进行了一次随机抽样问卷调查,其中有这样一个问题:
老师在课堂上放手让学生提问和表达 ()
A 从不;B 很少;C 有时;D 常常;E 总是
答题的学生在这五个选项中只能选择一项.下面是根据学生对该问题的答卷情况绘制的两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)该区共有名初二年级的学生参加了本次问卷调查;
(2)请把这幅条形统计图补充完整;
(3)在扇形统计图中,“总是”所占的百分比为.
已知:如图,AB为⊙O的直径,点C、D在⊙O上,且BC=6cm,AC=8cm,∠ABD=45º.
(1)求BD的长;
(2)求图中阴影部分的面积.