在平面直角坐标系xOy中，二次函数y＝mx2＋(m－3)x－3(m>0)的图象与x轴交于A、B两点（点A在点B左侧），与y轴交于点C求点A的坐标
当∠ABC＝45°时，求m的值
已知一次函数y＝kx＋b，点P(n，0)是x轴上的一个动点．在(2)的条件下，过点P垂直于x轴的直线交这个一次函数的图象于点M，交二次函数y＝mx2＋(m－3)x－3（m>0）的图象于点N．若只有当－2<n<2时，点M位于点N的上方，求这个一次函数的解析式
2008年5月12日，四川省发生8．0级地震，我校师生积极捐款，已知第一天捐款
4800元，第二天捐款6000元，第二天捐款人数比第一天捐款人数多50人，且两天人均捐款数相等，那么两天共参加捐款的人数是多少？
解方程
（1）
（2）
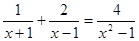
化简：
先化简代数式
，然后在取一组m，n的值代入求值
计算
（1）已知
，求
的值；
（2）若0＜x＜1，且
的值．
如图，已知点O在线段AB上，点C、D分别是AO、BO的中点
（1）AO= CO；BO= DO；
（2）若CO=3cm，DO=2cm，求线段AB的长度；
（3）若线段AB＝10，小明很轻松地求得CD=5．他在反思过程中突发奇想：若点O在线段AB的延长线上，原有的结论“CD=5”是否仍然成立呢？请帮小明画出图形分析，并说明理由．