汽车质量5t,为60KW,当汽车在水平路面上行驶时,受到的阻力是车重的0.1倍,g取10m/s2 ,问:
(1)汽车在此路面上行驶所能达到的最大速度是多少?
(2)若汽车从静止开始,保持以0.5m/s2的加速度作匀加速直线运动,这一过程能维持多长时间?
(3)若汽车从静止开始,保持额定功率做加速运动,10s后达到最大速度,求此过程中汽车的位移。
2012年10月4日,云南省彝良县发生特大泥石流,一汽车停在小山坡底,突然司机发现在距坡底240 m的山坡处泥石流以8 m/s的初速度、0.4 m/s2的加速度匀加速倾泻而下,假设泥石流到达坡底后速率不变,在水平地面上做匀速直线运动。已知司机的反应时间为1 s,汽车启动后以0.5 m/s2的加速度一直做匀加速直线运动。试分析汽车能否安全脱离?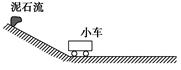
如图所示,把小车放在光滑的水平桌面上,用轻绳跨过定滑轮使之与盛有沙子的小桶相连,已知小车的质量为M,小桶与沙子的总质量为m,把小车从静止状态释放后,在小桶下落竖直高度为h的过程中,若不计滑轮及空气的阻力,求: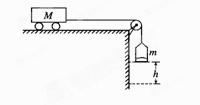
(1)下落过程中绳子的拉力大小;
(2)小桶下落h时的速度大小。
如图,人重600牛,木块A重400牛,人与A、A与地面间的动摩擦因数均为0.2,现人用水平力拉绳,使他与木块一起向右匀速直线运动,滑轮摩擦不计,求(1)人对绳的拉力.(2)人脚给A的摩擦力方向和大小。
2010·全国卷Ⅰ·24汽车由静止开始在平直的公路上行驶,0 ~60s内汽车的加速度随时/间变化的图线如右图所示。
⑴画出汽车在0~60s内的v-t图线;
⑵求在这60s内汽车行驶的路程。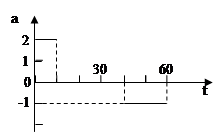
如图所示,质量为m,横截面为直角形的物快ABC,∠ABC=α,AB边靠在竖直墙上,F是垂直于斜面BC的推力,现物块静止不动,求摩擦力的大小。