(1)观察发现如题(a)图，若点A，B在直线
同侧，在直线上找一点P，使AP+BP的值最小． 做法如下：作点B关于直线的对称点
，连接
，与直线的交点就是所求的点P 再如题(b)图，在等边三角形ABC中，AB=2，点E是AB的中点，AD是高，在AD上找一点P，使BP+PE的值最小． 做法如下：作点B关于AD的对称点，恰好与点C重合，连接CE交AD于一点，则这点就是所求的点P，故BP+PE的最小值为 ．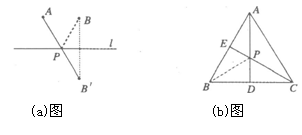 
(2)实践运用
如题(c)图，已知⊙O的直径CD为4，弧AD所对圆心角的度数为60°，点B是弧AD的中点，请你在直径CD上找一点P，使BP+AP的值最小，并求BP+AP的最小值．
(3)拓展延伸
如题(d)图，在四边形ABCD的对角线AC上找一点P，使∠APB=∠APD．保留
作图痕迹，不必写出作法．
在平面直角坐标系中，四边形OBCD是正方形，且D（0，2），点E是线段OB延长线上一点，M是线段OB上一动点（不包括点O、B），作MN⊥DM，垂足为M，交∠CBE的平分线于点N .
（1）写出点C的坐标；
（2）求证：MD = MN；
（3）连接DN交BC于点F，连接FM，下列两个结论：①FM的长度不变；②MN平分∠FMB，其中只有一个结论是正确的，请你指出正确的结论，并给出证明.
已知：在四边形ABCD中，AC = BD，AC与BD交于点O，∠DOC = 60°.
（1）当四边形ABCD是平行四边形时（如图1），证明AB + CD = AC；
（2）当四边形ABCD是梯形时（如图2），AB∥CD，线段AB、CD和线段AC之间的数量关系是____；
（3）如图3，四边形ABCD中，AB与CD不平行，结论AB + CD = AC是否仍然成立？如果成立，请给予证明；如果不成立，请说明理由.
若正整数a、b、c满足方程a2+b2=c2 ,则称这一组正整数（a、b、c）为“商高数”，下面列举五组“商高数”：（3，4，5），（5，12，13），（6，8，10），（7，24，25），（12，16，20），注意这五组“商高数”的结构有如下规律：
根据以上规律，回答以下问题：
（1）商高数的三个数中，有几个偶数，几个奇数？
（2）写出各数都大于30的两组商高数。
（3）用两个正整数m、n（m＞n）表示一组商高数，并证明你的结论。
已知关于x的一元二次方程x2＋4x＋m－1＝0。
(1)请你为m选取一个合适的整数，使得到的方程有两个不相等的实数根；
(2)设α、β是(1)中你所得到的方程的两个实数根，求α2＋β2＋αβ的值。
阅读材料:黑白双雄,纵横江湖;双剑合壁,天下无敌.这是武侠小说中的常见描述,其意指两个人合在一起,取长补短,威力无比.在二次根式中也有这样相辅相成的例子.
如
,
它们的积是有理数,我们说这两个二次根式互为有理化因式,其中一个是另一个的有理化因式.于是,二次根式除法可以这样解:
如
,
象这样,通过分子、分母同乘以一个式子把分母中的根号化去或根号中的分母化去，叫做分母有理化.
解决问题:
(1)
的有理化因式是. 
分母有理化得.
(2)分母有理化:(1) 
="_________;(2)" 
="________;(3)" 
=______.．
(3)计算: 
.