已知等差数列{ }中,
}中, 
求{ }前n项和
}前n项和 .
.
已知函数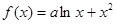 (
(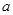 为实常数) .
为实常数) .
(1)当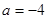 时,求函数
时,求函数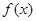 在
在 上的最大值及相应的
上的最大值及相应的 值;
值;
(2)当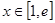 时,讨论方程
时,讨论方程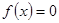 根的个数.
根的个数.
(3)若 ,且对任意的
,且对任意的 ,都有
,都有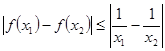 ,求实数a的取值范围.
,求实数a的取值范围.
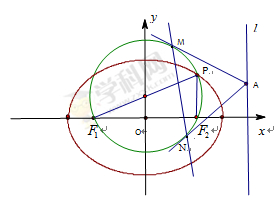
已知椭圆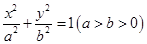 的左右两焦点分别为
的左右两焦点分别为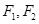 ,
,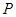 是椭圆上一点,且在
是椭圆上一点,且在 轴上方,
轴上方,
 .
.
(1)求椭圆的离心率 的取值范围;
的取值范围;
(2)当 取最大值时,过
取最大值时,过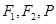 的圆
的圆 的截
的截 轴的线段长为6,求椭圆的方程;
轴的线段长为6,求椭圆的方程;
(3)在(2)的条件下,过椭圆右准线 上任一点
上任一点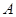 引圆
引圆 的两条切线,切点分别为
的两条切线,切点分别为 .试探究直线
.试探究直线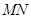 是否过定点?若过定点,请求出该定点;否则,请说明理由.
是否过定点?若过定点,请求出该定点;否则,请说明理由.
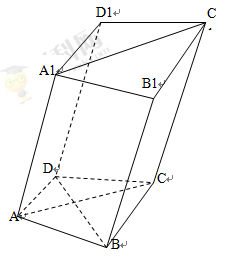
如图,在四棱柱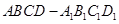 中,已知平面
中,已知平面 ,且
,且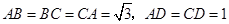 .
.
(1)求证: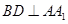 ;
;
(2)在棱BC上取一点E,使得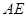 ∥平面
∥平面 ,求
,求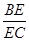 的值.
的值.
如图,过点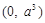 的两直线与抛物线
的两直线与抛物线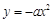 相切于A、B两点, AD、BC垂直于直线
相切于A、B两点, AD、BC垂直于直线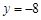 ,垂足分别为D、C.
,垂足分别为D、C.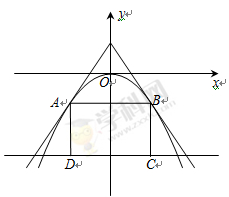
(1)若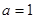 ,求矩形ABCD面积;
,求矩形ABCD面积;
(2)若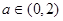 ,求矩形ABCD面积的最大值.
,求矩形ABCD面积的最大值.
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,DC∥AB,∠BAD=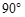 ,且AB=2AD=2DC=2PD=4,E为PA的中点.
,且AB=2AD=2DC=2PD=4,E为PA的中点.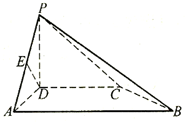
(1)证明:DE∥平面PBC;
(2)证明:DE⊥平面PAB.