如图,已知△ABC中,AB=AC=10厘米,BC=8厘米,点D为AB的中点.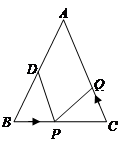
(1)如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动,设运动的时间为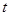 秒.
秒.
①当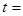 1秒时,则BP= 厘米;
1秒时,则BP= 厘米;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD≌△CPQ,并求全等时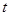 的值.
的值.
(2)若点Q以②中的运动速度从点C出发,点P以(1)中的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?
如图,在直角梯形纸片 中,
中,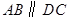 ,
,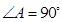 ,
,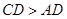 ,将纸片沿过点
,将纸片沿过点 的直线折叠,使点
的直线折叠,使点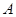 落在边
落在边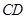 上的点
上的点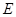 处,折痕为
处,折痕为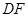 .连接
.连接 并展开纸片.
并展开纸片.
(1)求证:四边形 是正方形;
是正方形;
(2)取线段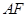 的中点
的中点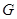 ,连接
,连接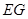 ,如果
,如果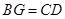 ,试说明四边形
,试说明四边形 是等腰梯形.
是等腰梯形.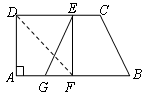
化简代数式( -4)÷
-4)÷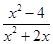 ,当
,当 满足
满足 ,且x为正整数时,求代数式的值.
,且x为正整数时,求代数式的值.
(1)计算: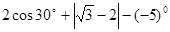 ;(2)解方程
;(2)解方程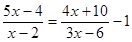 .
.
如图,在平面直角坐标系中,点O为坐标原点,直线y=﹣x+n与x轴、y轴分别交于B、C两点,抛物线y=ax2+bx+3(a≠0)过C、B两点,交x轴于另一点A,连接AC,且tan∠CAO=3.
(1)求抛物线的解析式;
(2)若点P是射线CB上一点,过点P作x轴的垂线,垂足为H,交抛物线于Q,设P点横坐标为t,线段PQ的长为d,求出d与t之间的函数关系式,并写出相应的自变量t的取值范围;
(3)在(2)的条件下,当点P在线段BC上时,设PH=e,已知d,e是以y为未知数的一元二次方程:y2-(m+3)y+ (5m2-2m+13)="0" (m为常数)的两个实数根,点M在抛物线上,连接MQ、MH、PM,且.MP平分∠QMH,求出t值及点M的坐标.
(5m2-2m+13)="0" (m为常数)的两个实数根,点M在抛物线上,连接MQ、MH、PM,且.MP平分∠QMH,求出t值及点M的坐标.
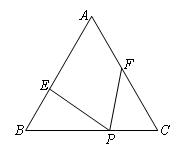
已知,等边△ABC边长为6,P为BC边上一点,且BP=4,点E、F分别在边AB、AC上,且∠EPF=60°,设BE=x,CF=y.
(1)求y与x的函数关系式,并写出x的取值范围;
(2)①若四边形AEPF的面积为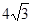 时,求x的值.
时,求x的值.
②四边形AEPF的面积是否存在最大值?若存在,请求出面积的最大值及此时x的值;若不存在,请说明理由.