“校园手机”现象越来越受到社会的关注.小丽在“统计实习”活动中随机调查了学校若干名学生家长对“中学生带手机到学校”现象的看法,统计整理并制作了如下的统计图:
求这次调查的家长总数及家长表示“无所谓”的人数,并补全图①;
求图②中表示家长“无所谓”的圆心角的度数;
从这次接受调查的家长中,随机抽查一个,恰好是“不赞成”态度的家长的概率是多少
黄商超市以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件.超市为增加销售量,决定降价销售,根据市场调查,单价第降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,超市将对剩余的T恤一次性清仓销售,清仓时单价为40元,设第二个月单价降低x元.
(1)完成下表(不化简)
| 时间 |
第一个月 |
第二个月 |
清仓时 |
| 单价(元) |
80 |
40 |
|
| 销售量(件) |
200 |
(2)如果超市希望通过销售这批T恤获利9000元,那么第二个月的单价是多少元?
解下列方程(1)4x²-4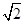 x+1=0
x+1=0
(2)(3x+2)²=(5-2x)²
已知,如图,在平面直角坐标系中,Rt△ABC的斜边BC在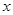 轴上,直角顶点A在
轴上,直角顶点A在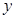 轴的正半轴上,A(0,2),B(-1,0)。
轴的正半轴上,A(0,2),B(-1,0)。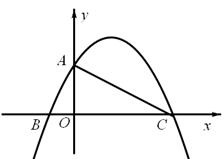
(1)求点C的坐标并求过A、B、C三点的抛物线的解析式
(2)设点P(m,n)是抛物线在第一象限部分上的点,△PAC的面积为S,求S关于m的函数关系式,并求使S最大时点P的坐标.;
(3)在抛物线的对称轴上是否存在点Q,使△QAC是以AC为腰的等腰三角形?如果存在,直接写出Q点的坐标;如果不存在,请说明理由;
如图,在Rt△ABC中,∠ACB=90°,D是AB边上一点,以BD为直径的⊙O与AC交于点E,连接DE并延长,与BC的延长线交于点F,BD=BF.
(1)求证:AC是⊙O的切线;
(2)若BC=12,AD=8,求 的长.
的长.
已知一元二次方程 的一根为2.
的一根为2.
(1)求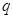 关于
关于 的关系式;
的关系式;
(2)若 ,求方程的另一根;
,求方程的另一根;
(3)求证:抛物线 与
与 轴有两个交点.
轴有两个交点.