有3张扑克牌,分别是红桃3、红桃4和黑桃5.把牌洗匀后甲先抽取一张,记下花色和数字后将牌放回,洗匀后乙再抽取一张.先后两次抽得的数字分别记为s和t,则︱s-t︱≥1的概率
甲、乙两人做游戏,现有两种方案.A方案:若两次抽得相同花色则甲胜,否则乙胜.B方案:若两次抽得数字和为奇数则甲胜,否则乙胜.请问甲选择哪种方案胜率更高?
已知二次函数y=x2-(m+3)x+2m-1.
(1)证明:无论m取何值时,其图象与x轴总有两个交点;
(2)当其图象与y轴交于点A(0,5)时,求m的值;
(3)设由(2)确定的二次函数的图象与x轴自左向右依次交于点B、C,顶点为D,直线y=kx.
①问是否存在k的值,使得直线y=kx既平分△AOD的面积,又平分它的周长?若存在,求出k的值;若不存在,请说明理由;
②设直线y=kx与AD相交于点P,问是否存在以O、P、A(或D)为顶点的三角形与△OAD相似?若存在,求出P点的坐标;若不存在,请说明理由.
小明在一次数学兴趣小组活动中,对一个数学问题作如下探究:
问题情境:如图1,四边形ABCD中,AD∥BC,点E为DC边的中点,连接AE并延长交BC的延长线于点F,求证:S四边形ABCD=S△ABF.(S表示面积)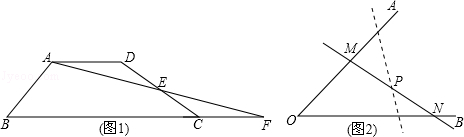
问题迁移:如图2:在已知锐角∠AOB内有一个定点P.过点P任意作一条直线MN,分别交射线OA、OB于点M、N.小明将直线MN绕着点P旋转的过程中发现,△MON的面积存在最小值,请问当直线MN在什么位置时,△MON的面积最小,并说明理由.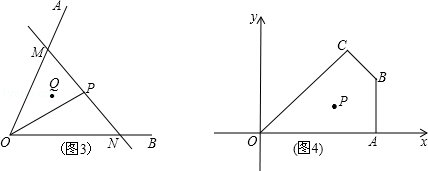
实际应用:如图3,若在道路OA、OB之间有一村庄Q发生疫情,防疫部门计划以公路OA、OB和经过防疫站P的一条直线MN为隔离线,建立一个面积最小的三角形隔离区△MON.若测得∠AOB=66°,∠POB=30°,OP=4km,试求△MON的面积.(结果精确到0.1km2)(参考数据:sin66°≈0.91,tan66°≈2.25,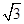 ≈1.73)
≈1.73)
拓展延伸:如图4,在平面直角坐标系中,O为坐标原点,点A、B、C、P的坐标分别为(6,0)(6,3)(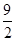 ,
,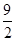 )、(4、2),过点p的直线l与四边形OABC一组对边相交,将四边形OABC分成两个四边形,求其中以点O为顶点的四边形面积的最大值.
)、(4、2),过点p的直线l与四边形OABC一组对边相交,将四边形OABC分成两个四边形,求其中以点O为顶点的四边形面积的最大值.
回顾旧知:在探究有关正多边形的有关性质时,我们是从那几个方面展开的?探究的方法与过程又是怎样的?(不要求回答)
温馨提示,如图1,是一个边长为a的正六边形.我们知道它具有如下的性质:①正六边形的每条边长度相等;②正六边形的六个内角相等,都是120°;③正六边形的内角和为720°;④正六边形的外角和为360°.等.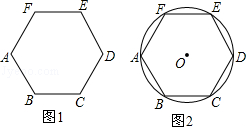
解答问题:
(1)观察图2,请你在下面的横线上,再写出边长为a的正六边形所具有不同于上述的性质(不少于5条): .
(2)尺规作图:在图2中作出圆内接正六边形的内切圆(不要求写作法,只保留作图痕迹);
(3)求出这个正六边形外接圆半径与内切圆半径的比值.
如图,在东西方向的海岸线l上有一长为1千米的码头MN,在码头西端M的正西方向30 千米处有一观察站O.某时刻测得一艘匀速直线航行的轮船位于O的北偏西30°方向,且与O相距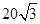 千米的A处;经过40分钟,又测得该轮船位于O的正北方向,且与O相距20千米的B处.
千米的A处;经过40分钟,又测得该轮船位于O的正北方向,且与O相距20千米的B处.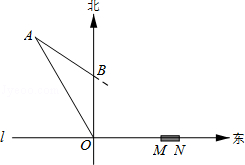
(1)求该轮船航行的速度;
(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由.(参考数据: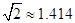 ,
,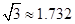 )
)
我校实行学案教学,需印刷若干份数学学案.印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要.两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示: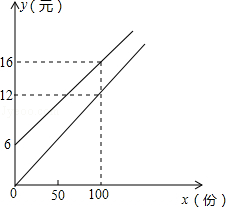
(1)填空:
甲种收费方式的函数关系式是y1= ;
乙种收费方式的函数关系式是y2= ;
(2)如果我校2014-2015学年八年级每次印刷100~450(含100和450)份学案,选择哪种印刷方式较合算.