爱动脑筋的小明制造了一个小黑匣,只要你输入一个数字,它就输出另一个数来,好奇心强的小亮赶紧试试了一下,结果得到了下面的表格
| 输入 |
2 |
5 |
10 |
17 |
26 |
37 |
… |
| 输出 |
1 |
… |
聪明的你一定知道当输入的数是65时,输出的结果是
阅读理解:
如图①,图形 外一点 与图形 上各点连接的所有线段中,若线段 最短,则线段 的长度称为点 到图形 的距离.
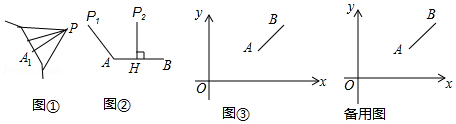
例如:图②中,线段 的长度是点 到线段 的距离;线段 的长度是点 到线段 的距离.
解决问题:
如图③,平面直角坐标系 中,点 、 的坐标分别为 , ,点 从原点 出发,以每秒1个单位长度的速度向 轴正方向运动了 秒.
(1)当 时,求点 到线段 的距离;
(2) 为何值时,点 到线段 的距离为5?
(3) 满足什么条件时,点 到线段 的距离不超过6?(直接写出此小题的结果)
怡然美食店的 、 两种菜品,每份成本均为14元,售价分别为20元、18元,这两种菜品每天的营业额共为1120元,总利润为280元.
(1)该店每天卖出这两种菜品共多少份?
(2)该店为了增加利润,准备降低 种菜品的售价,同时提高 种菜品的售价,售卖时发现, 种菜品售价每降0.5元可多卖1份; 种菜品售价每提高0.5元就少卖1份,如果这两种菜品每天销售总份数不变,那么这两种菜品一天的总利润最多是多少?
平面直角坐标系 中,点 的坐标为 .
(1)试判断点 是否在一次函数 的图象上,并说明理由;
(2)如图,一次函数 的图象与 轴、 轴分别相交于点 、 ,若点 在 的内部,求 的取值范围.

“泰微课”是学生自主学习的平台,某初级中学共有1200名学生,每人每周学习的数学泰微课都在6至30个之间(含6和30),为进一步了解该校学生每周学习数学泰微课的情况,从三个年级随机抽取了部分学生的相关学习数据,并整理、绘制成统计图如下:
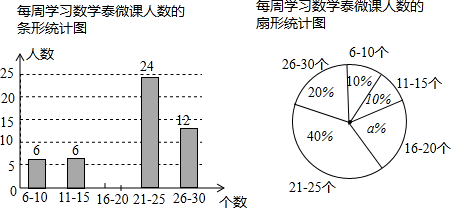
根据以上信息完成下列问题:
(1)补全条形统计图;
(2)估计该校全体学生中每周学习数学泰微课在16至30个之间(含16和30)的人数.
(1)计算: ;
(2)解方程: .