一个袋子中有大小相同的2个红球和3个黑球,从袋中随机地取球,取到每个球的可能性是相同的,设取到一个红球得2分,取到一个黑球得1分。
(1)若从袋子中一次取出3个球,求得4分的概率;
(2)若从袋子中每次摸出一个球,看清颜色后放回,连续摸2次,求所得分数的分布列及数学期望。
某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下图所示.
(I)请先求出频率分布表中①、②位置相应数据,再在答题纸上完成下列频率分布直方图;
(Ⅱ)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(Ⅲ)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官的面试,求:第4组至少有一名学生被考官A面试的概率?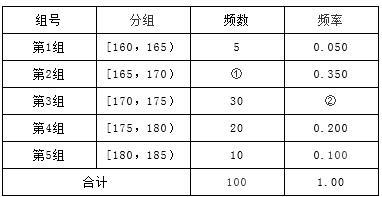
甲、乙两位学生参加数学竞赛培训,在培训期间,他们参加的5次预赛成绩记录如下:
甲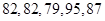
乙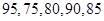
(1)用茎叶图表示这两组数据;
(2)从甲、乙两人的成绩中各随机抽取一个,求甲的成绩比乙高的概率;
(3)①求甲、乙两人的成绩的平均数与方差,②若现要从中选派一人参加数学竞赛,根据你的计算结果,你认为选派哪位学生参加合适?
已知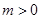 ,
,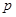 :
: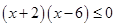 ,
,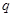 :
: .
.
(I)若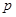 是
是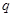 的充分条件,求实数
的充分条件,求实数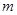 的取值范围;
的取值范围;
(Ⅱ)若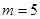 ,“
,“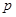 或
或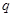 ”为真命题,“
”为真命题,“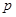 且
且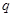 ”为假命题,求实数
”为假命题,求实数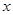 的取值范围
的取值范围
(本题12分)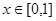 时,求函数
时,求函数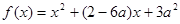 的最小值
的最小值
(本题12分)已知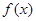 是定义在
是定义在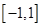 的增函数,
的增函数,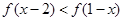 ,求
,求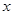 的取值范围
的取值范围