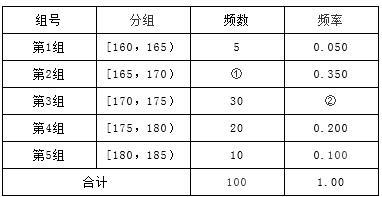
某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下图所示.
(I)请先求出频率分布表中①、②位置相应数据,再在答题纸上完成下列频率分布直方图;
(Ⅱ)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(Ⅲ)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官的面试,求:第4组至少有一名学生被考官A面试的概率?
(本小题满分12分)某校从6名学生会干部(其中男生4人,女生2人)中选3人参加市中学生运动会志愿者。(Ⅰ)所选3人中女生人数为ξ,求ξ的分布列及数学期望。
(Ⅱ)在男生甲被选中的情况下,求女生乙也被选中的概率
(本小题满分12分) 已知向量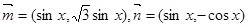 ,设函数
,设函数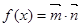 ,(Ⅰ)求函数
,(Ⅰ)求函数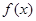 的表达式;(Ⅱ)在
的表达式;(Ⅱ)在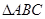 中,
中,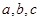 分别是角
分别是角 的对边,
的对边,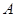 为锐角,若
为锐角,若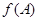
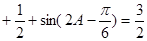 ,
,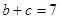 ,
,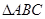 的面积为
的面积为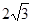 ,求边
,求边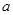 的长.
的长.
集合A是由适合以下性质的函数f(x)构成的:对于定义域内任意两个不相等的实数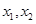 ,都有
,都有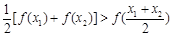 .
.
(1)试判断f(x)= x2及g(x)=log2x是否在集合A中,并说明理由;
(2)设f(x)ÎA且定义域为(0,+¥),值域为(0,1),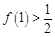 ,试求出一个满足以上条件的函数f (x)的解析式.
,试求出一个满足以上条件的函数f (x)的解析式.
(本小题满分14分)
已知 ,设
,设 :函数
:函数 在R上单调递减;
在R上单调递减; :函数
:函数 的图象与x轴至少有一个交点.如果P与Q有且只有一个正确,求
的图象与x轴至少有一个交点.如果P与Q有且只有一个正确,求 的取值范围.
的取值范围.
已知函数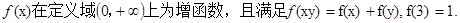
(1)
(2)