已知函数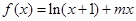 ,当
,当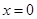 时,函数
时,函数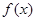 取得极大值.
取得极大值.
(1)求实数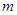 的值;
的值;
(2)已知结论:若函数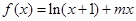 在区间
在区间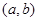 内导数都存在,且
内导数都存在,且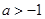 ,则存在
,则存在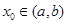 ,使得
,使得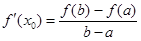 .试用这个结论证明:若
.试用这个结论证明:若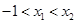 ,函数
,函数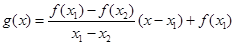 ,则对任意
,则对任意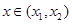 ,都有
,都有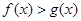 ;
;
(3)已知正数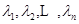 ,满足
,满足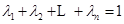 ,求证:当
,求证:当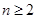 ,
,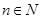 时,对任意大于
时,对任意大于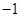 ,且互不相等的实数
,且互不相等的实数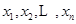 ,都有
,都有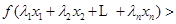
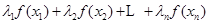 .
.
已知椭圆: 的左右焦点分别为
的左右焦点分别为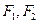 ,离心率为
,离心率为 ,两焦点与上下顶点形成的菱形面积为2.
,两焦点与上下顶点形成的菱形面积为2.
(Ⅰ)求椭圆的方程;
(Ⅱ)过点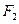 的直线
的直线 与椭圆交于A, B两点,四边形
与椭圆交于A, B两点,四边形 为平行四边形,
为平行四边形,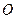 为坐标原点,且
为坐标原点,且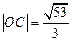 ,求直线
,求直线 的方程.
的方程.
如图,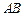 为圆
为圆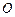 的直径,点
的直径,点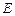 、
、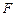
在圆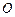 上,且
上,且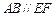 ,矩形
,矩形 所在的平面和圆
所在的平面和圆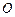
所在的平面 互相垂直,且
互相垂直,且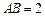 ,
,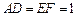 .
.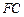 的
的
中点为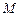 .
.
(Ⅰ)求证: 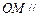 平面
平面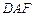 ;
;
(Ⅱ)求二面角A—CF—E的大小;
(Ⅲ)求三棱锥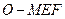 的体积.
的体积.
南充高中组织了一次趣味运动会,奖品为肥皂或洗衣服.新老校区共36名教师参加,其中 是新校区的老师,其余是老校区的老师.在新校区的参加者中有
是新校区的老师,其余是老校区的老师.在新校区的参加者中有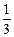 获得一块肥皂的奖励,在老校区的参加者中有
获得一块肥皂的奖励,在老校区的参加者中有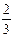 获得一袋洗衣粉的奖励,其余人没有获奖.
获得一袋洗衣粉的奖励,其余人没有获奖.
(I)在参加运动会的教师中随机采访3人,求恰有1人获得肥皂且获得洗衣粉的教师少于2人的概率;
(II)在老校区参加运动会的教师中随机采访3人,分别求获得洗衣粉的人数为1人和3人的概率.
已知向量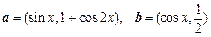 ,定义函数
,定义函数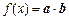
(I)求函数 最小正周期;
最小正周期;
(II)在△ABC中,角A为锐角,且 ,求边AC的长.
,求边AC的长.
甲有一个箱子,里面放有x个红球,y个白球(x,y≥0,且x+y=4);乙有一个箱子,里面放有2个红球,1个白球,1个黄球.现在甲从箱子里任取2个球,乙从箱子里任取1个球.若取出的3个球颜色全不相同,则甲获胜.
(1)试问甲如何安排箱子里两种颜色球的个数,才能使自己获胜的概率最大?
(2)在(1)的条件下,求取出的3个球中红球个数的期望.