已知函数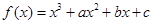
在
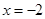处取得极值,并且
它的图象与直线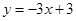
在点( 1 , 0 ) 处相切, 求a , b , c的值。
设函数
（1）写出函数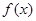
的最小正周期及单调递减区间；
（2）当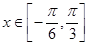
时，函数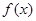的最大值与最小值的和为
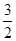，求不等式
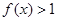的解集．
设关于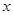
的一元二次方程
.
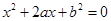（1）若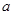
，
都是从集合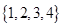
中任取的数字，求方程有实根的概率；
（2）若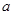是从区间[0,4]中任取的数字，是从区间[1，4]中任取的数字，求方程有实根的概率．
已知数列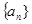
的前n项和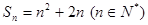
．
（1）求数列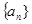的通项公式；
（2）若数列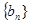
是等比数列，公比为
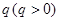，且满足
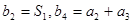，求数列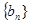的前n项和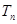
．
(本题满分10分)选修4 - 5 ：不等式选讲
设函数，
.
(I)求证
；
(II)若
成立，求x的取值范围.
(本题满分10分)选修4－4 ：坐标系与参数方程
将圆
上各点的纵坐标压缩至原来的
，所得曲线记作C;将直线3x-2y-8=0
绕原点逆时针旋转90°所得直线记作l
.(I)求直线l与曲线C的方程；
(II)求C上的点到直线l的最大距离.