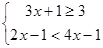某牛奶加工厂现有鲜奶10吨,若在市场上直接销售,每吨可获取利润500元,制成酸奶销售,每吨可获利润1200元,制成奶片销售,每吨可获利润2000元,该工厂的生产能力为:如制成酸奶,每天可加工3吨,制成奶片每天可加工1吨,受人员限制,两种加工方式不能同时进行,受气温条件限制,这批牛奶必须在4天内全部销售或加工完毕,为此,该加工厂设计了两种可行性方案:
方案一:尽可能多的制成奶片,其余直接销售鲜牛奶。
方案二:将一部分制成奶片,其余制成酸奶销售,并恰好4天完成。
你认为选择哪种方案获利最多,为什么。(本题12分)
初一年级师生外出春游,若每辆车坐45人,则恰好少1辆车;若辆车坐54人,则只有一辆车没有坐满,但超过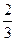 。问有多少辆车?多少名师生?(本题12分)
。问有多少辆车?多少名师生?(本题12分)
小华参加了若干次考试,若最后一次考试得97分,则平均分为90分 ;若最后一次考
;若最后一次考 试得73分,则平均分为87分。问小华参加了多少次考试?(本题12分)
试得73分,则平均分为87分。问小华参加了多少次考试?(本题12分)
已知x满足 ,试化简
,试化简 。 (本题12分)
。 (本题12分)