在形如 的式子中,我们已经研究过两种情况:①已知a和b,求N,这是乘方运算;②已知b和N,求a,这是开方运算;
的式子中,我们已经研究过两种情况:①已知a和b,求N,这是乘方运算;②已知b和N,求a,这是开方运算;
现在我们研究第三种情况:已知a和N,求b,我们把这种运算叫做对数运算。
定义:如果 (a>0,a≠1,N>0),则b叫做以a为底N的对数,记作:
(a>0,a≠1,N>0),则b叫做以a为底N的对数,记作: ,例如:求
,例如:求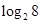 ,因为
,因为 =8,所以
=8,所以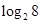 =3;又比如∵
=3;又比如∵ ,∴
,∴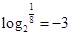 .
.根据定义计算:(本小题6分)
①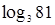 =____;②
=____;②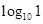 = ;
= ;
③如果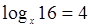 ,那么x= 。
,那么x= 。设
 则
则 (a>0,a≠1,M、N均为正数),
(a>0,a≠1,M、N均为正数),
∵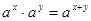 ,∴
,∴ ∴
∴ ,
,
即
这是对数运算的重要性质之一,进一步,我们还可以得出: = .(其中M1、M2、M3、……、Mn均为正数,a>0,a≠1)(本小题2分)
= .(其中M1、M2、M3、……、Mn均为正数,a>0,a≠1)(本小题2分)请你猜想:
 (a>0,a≠1,M、N均为正数).(本小题2分)
(a>0,a≠1,M、N均为正数).(本小题2分)
如图,分别按下列要求作出经平移所得的图形.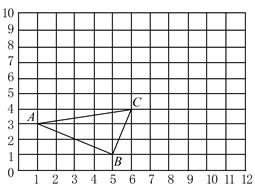
(1)将三角形ABC向上平移4个单位得三角形A1B1C1;
(2)把第(1)题中平移所得的图形向右平移5个单位得三角形A2B2C2;
(3)经(1)(2)两题两次平移后所得的图形,能通过将三角形ABC经过一次平移得到吗?如果你认为可以,请简单描述这个平移过程.
如图,已知DE、BF分别平分∠ADC和∠ABC,∠1=∠2,∠ADC=∠ABC,由此可以推出图中哪些线段平行?请说明理由. 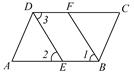
如图,已知AB∥CD,DF平分∠CDE,交AB于F,且∠2=68º,求出∠1,∠3的度数.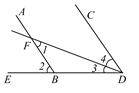
解方程组:(1)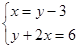 ;(2)
;(2)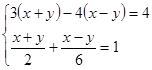
如图,已知EF∥AD,∠1=∠2,∠BAC=65º.请将求∠AGD的过程填写完整.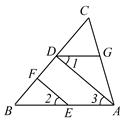
解:∵EF∥AD
∴∠2= ( )
又∵∠1=∠2
∴∠1=∠3
∴AB∥ ( )
∴∠BAC+ =180º.
又∵∠BAC=65º
∴∠AGD= .