为了美化宁波城区各景观河道、改善内河水环境，需对内河进行清理。现有一段长为180米的河道整治任务由A、B两个工程队先后接力完成。A工程队每天整治12米，B工程队每天整治8米，共用时20天。
根据题意，甲、乙两个同学分别列出了尚不完整的方程组如下：
根据甲、乙两名同学所列的方程组，请你分别指出未知数x,y表示的意义，然后在方框中补全甲、乙两名同学所列的方程组：
甲：x表示 ，y表示 ；
乙：x表示 ，y表示 ；
求A、B两工程队分别整治河道多少米？（写出完整的解答过程）
某人用400元购买了8套儿童服装，准备以一定价格出售，如果以每套儿童服装55元的价格为标准，超出的记作正数，不足的记作负数，记录如下：
＋2，—3，＋2，＋1，—2，—1，0，—2．（单位：元）
（1）当他卖完这八套儿童服装后是盈利还是亏损？
（2）盈利（或亏损）了多少钱？
在边长为16cm的正方形纸片的四个角各剪去一个同样大小的正方形，折成一个无盖的长方体．
（1）如果剪去的小正方形的边长为xcm，请用含x的代数式来表示这个无盖长方体的体积；
（2）当剪去的小正方形的边长x的值分别为3cm和3．5cm时，比较折成的无盖长方体的体积的大小．
先化简，再求值：
，其中
．
画一条数轴，并在数轴上表示：3．5和它的相反数，－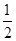
和它的倒数，绝对值等于3的数，并把这些数由小到大用“<”号连接起来．
若|a|=4，|b|=2，且a＜b，求a－b的值．