已知 是定义在R上的函数,
是定义在R上的函数, ,
,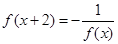 。
。
(1)函数 是不是周期函数,若是,求出周期。
是不是周期函数,若是,求出周期。
(2)判断 的奇偶性
的奇偶性
(本小题满分12分)已知向量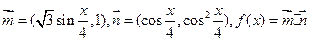 。
。
(1)若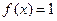 ,求
,求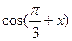 的值;
的值;
(2)在△ABC中,角A、B、C的对边分别是a、b、c,且满足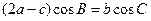 ,
,
求函数 的取值范围。
的取值范围。
已知构成某系统的元件能正常工作的概率为p(0<p<1),且各个元件能否正常工作是相互独立的.今有2n(n大于1)个元件可按下图所示的两种联结方式分别构成两个系统甲、乙.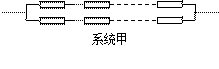
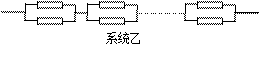
(1)试分别求出系统甲、乙能正常工作的概率p1,p2;
(2)比较p1与p2的大小,并从概率意义上评价两系统的优劣.
如图,在四棱锥O-ABCD中,底面ABCD是边长为1的菱形,∠ABC=45°,OA⊥底面ABCD,OA=2,M为OA的中点.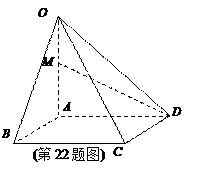
(1)求异面直线AB与MD所成角的大小;
(2)求平面OAB与平面OCD所成二面角的余弦值.
A.选修4-1:几何证明选讲
|
(本小题满分10分)
如图,设AB为⊙O的任一条不与直线l垂直的直径,P是⊙O与l的公共点,AC⊥l,BD⊥l,垂足分别为C,D,且PC=PD.求证:(1)l是⊙O的切线;(2)PB平分∠ABD.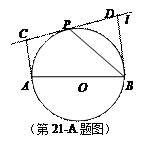
设数列{an}满足:a1=1,a2=2,an+2=(n≥1,nÎN*).
(1)求证:数列{}是常数列;
(2)求证:当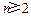 时,2<a-a≤3;
时,2<a-a≤3;
(3)求a2011的整数部分