按照要求写出下列形式的命题的
(1)“末位数字是0或5的整数能被5整除”的否命题;
(2)“任何实数x都是方程5x-12=0的根”的否定;
(3)“对于任意实数x,存在实数y,使x+y>0”的否定
(4)“若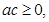 则二次方程
则二次方程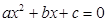 没有实根”的逆否命题
没有实根”的逆否命题
选修4-1:几何证明选讲
如图,圆O的直径AB=10,弦DE⊥AB于点H,AH=2。
(1)求DE的长;
(2)延长ED到P,过P作圆O的切线,
切点为C,若PC=2 ,求PD的长。
,求PD的长。
(本小题满分14分)
等差数列 的各项均为正数,
的各项均为正数,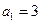 ,前
,前 项和为
项和为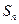
 ,
,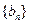 为等比数列,
为等比数列, 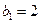 ,且
,且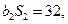
 .
.
(1)求 与
与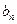 ;
;
(2)求数列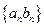 的前
的前 项和
项和 。
。
(3)若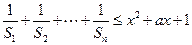 对任意正整数
对任意正整数 和任意
和任意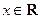 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分14分)
已知函数
(1)若 ,求
,求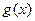
 的单调递减区间;
的单调递减区间;
(2)若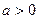 ,且存在
,且存在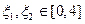 使得
使得 ,求实数
,求实数 的取值范围。
的取值范围。
已知角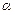 的顶点在原点,始边与
的顶点在原点,始边与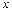 轴的正半轴重合,终边经过点
轴的正半轴重合,终边经过点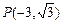 .
.
(1)求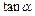 的值;
的值;
(2)定义行列式运算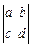
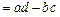 ,求行列式
,求行列式 的值;
的值;
(3)若函数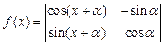 (
( ),求函数
),求函数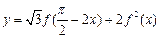 的最大值,并指出取到最大值时
的最大值,并指出取到最大值时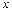 的值.
的值.
本题满分10分)
设向量 =
= ,
, =
=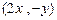 (其中实数
(其中实数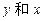 不同时为零),当
不同时为零),当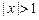 时,有
时,有 ;当
;当 时,有
时,有 ∥
∥ .
.
(1)求函数解析式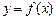 ;
;
(2)设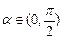 ,且
,且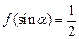 ,求sin
,求sin .
.