我们把能平分四边形面积的直线称为“好线”.利用下面的作图，可以得到四边形的“好线”：如图1，在四边形ABCD中，取对角线BD的中点O，连结OA、OC. 显然，折线AOC能平分四边形ABCD的面积，再过点O作OE∥AC交CD于E，则直线AE即为一条“好线”.
（1）试说明直线AE是“好线”的理由；
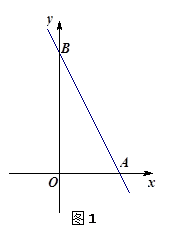
（2）如图2，AE为一条“好线”，F为AD边上的一点，请作出经过F点的“好线”，只需对画图步骤作适当说明（不需要说明“好线”的理由）.
计算：
计算：
计算：（
－
）×
如图1，在平面直角坐标系中，A（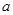
，0），B（0，
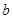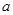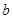），且、满足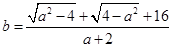
.
（1）求直线AB的解析式；
（2）若点M为直线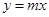
在第一象限上一点，且△ABM是等腰直角三角形，求
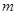的值.
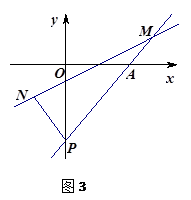
（3）如图3过点A的直线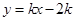
交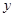
轴负半轴于点P，N点的横坐标为-1，过N点的直线
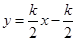交AP于点M，给出两个结论：①
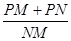的值是不变；②
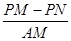的值是不变，只有一个结论是正确，请你判断出正确的结论，并加以证明和求出其值。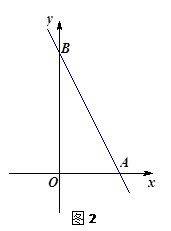
已知△ABC是等边三角形，点P是AC上一点，PE⊥BC于点E，交AB于点F，在CB的延长线上截取BD=PA，PD交AB于点I，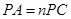
.
（1）如图1，若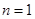
，则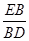
= ，
= ；
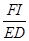（2）如图2，若∠EPD=60º，试求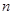
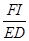和的值；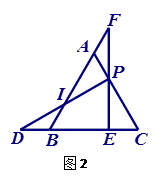
（3）如图3，若点P在AC边的延长线上，且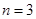
，其他条件不变，则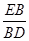= .(只写答案不写过程)