阅读：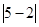 
表示5与2差的绝对值，也可理解为5与2两数在数轴上所
对应的两点之间的距离；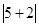
可以看做
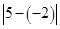，表示5与－2的差的绝对值，也
可理解为5与－2两数在数轴上所对应的两点之间的距离．
探索: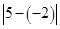=___________利用数轴，找出所有符合条件的整数
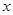，使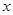所表示的点到5和—2的距离之和为7由以上探索猜想，对于任何有理数
，
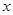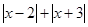是否有最小值? 如果有，写出最
小值；如果没有，说明理由
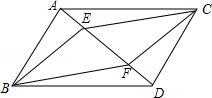
如图，在平行四边形ABCD中，对角线AC、BD相交于点O，AF⊥BD，CE⊥BD，垂足分别为E、F；连结AE、CF，得四边形AFCE，试判断四边形AFCE是下列图形中的哪一种？①平行四边形；②菱形；③矩形；请证明你的结论.
如图，正方形ABCD中，E、F分别为CD、DA的中点，BE、CF交于P，求证AP=AB。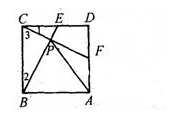
如图，在等腰Rt△ABC与Rt△ABD中，∠ABC=∠BAD=90°，AD=BC，AC，BD相交于点G，过点A作AE∥DB交CB的延长线于点E，过点B作BF∥CA交DA的延长线于点F，AE，BF相交于点H。判断四边形AHBG的形状。
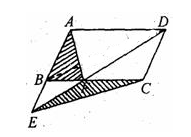
如图，E是平行四边形ABCD中AB延长线上一点，ED交BC于F，求证：
。
已知：如图，在平行四边形ABCD中，点E、F在AC上，且AE=DF．
求证：四边形BECF是平行四边形．