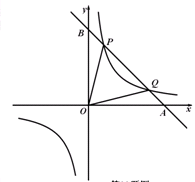
如图,已知反比例函数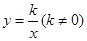 的图象经过点(
的图象经过点(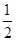 ,8),直线
,8),直线 经过该反比例函数图象上的点Q(4,
经过该反比例函数图象上的点Q(4,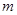 ).
).
求上述反比例函数和直线的函数表达式;
设该直线与
 轴、
轴、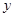 轴分别相交于A 、B两点,与反比例函数图象的另一个交点为P,连结0P、OQ,求△OPQ的面积.
轴分别相交于A 、B两点,与反比例函数图象的另一个交点为P,连结0P、OQ,求△OPQ的面积.
已知抛物线 经过点 ,当 时, 随 的增大而增大,当 时, 随 的增大而减小.设 是抛物线 与 轴的交点(交点也称公共点)的横坐标, .
(1)求 、 的值;
(2)求证: ;
(3)以下结论: , , ,你认为哪个正确?请证明你认为正确的那个结论.
如图, 是 的直径,点 是 上异于 、 的点,连接 、 ,点 在 的延长线上,且 ,点 在 的延长线上,且 .
(1)求证: 是 的切线;
(2)若 , ,求 的长.

某鲜花销售公司每月付给销售人员的工资有两种方案.
方案一:没有底薪,只付销售提成;
方案二:底薪加销售提成.
如图中的射线 ,射线 分别表示该鲜花销售公司每月按方案一,方案二付给销售人员的工资 (单位:元)和 (单位:元)与其当月鲜花销售量 (单位:千克) 的函数关系.
(1)分别求 、 与 的函数解析式(解析式也称表达式);
(2)若该公司某销售人员今年3月份的鲜花销售量没有超过70千克,但其3月份的工资超过2000元.这个公司采用了哪种方案给这名销售人员付3月份的工资?

如图,四边形 是矩形, 、 分别是线段 、 上的点,点 是 与 的交点.若将 沿直线 折叠,则点 与点 重合.
(1)求证:四边形 是菱形;
(2)若 , ,求 的值.

为庆祝中国共产党成立100周年,某市组织该市七、八两个年级学生参加演讲比赛,演讲比赛的主题为“追忆百年历程,凝聚青春力量”.该市一中学经过初选,在七年级选出3名同学,其中2名女生,分别记为 、 ,1名男生,记为 ;在八年级选出3名同学,其中1名女生,记为 ,2名男生,分别记为 、 .现分别从两个年级初选出的同学中,每个年级随机选出一名同学组成代表队参加比赛.
(1)用列表法或树状图法(树状图也称树形图)中的一种方法,求所有可能出现的代表队总数;
(2)求选出的代表队中的两名同学恰好是一名男生和一名女生的概率 .