(1)如图1,已知△ABC,以边AB、AC为边分别向外作等边三角形ABD和等边三角形ACE,连接CD、BE.求证:⑴CD=BE.
(2)如图2,已知△ABC,以边AB、AC为边分别向外作正方形ABFD和正方形ACGE,连接CD、BE,CD与BE有什么数量关系?(直接写结果,不需要过程).
(3)运用(1)、(2)解答中所积累的经验和知识,完成下题:
如图3,要测量池塘两岸相对的两点B、E的距离,已经测得∠ABC=45°,∠CAE=90°,AB=BC=100米,AC=AE,求BE的长.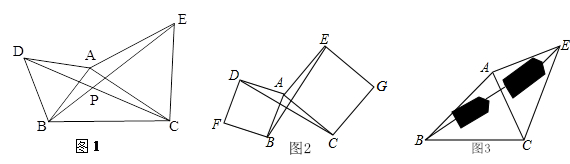
如图,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=16,DC=12,AD=21。动点P从点D出发,沿射线DA的方向以每秒2两个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P,Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动。设运动的时间为t(秒).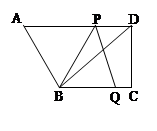
(1)设△BPQ的面积为S,求S与t之间的函数关系式
(2)当线段PQ与线段AB相交于点O,且2AO=OB时,求t的值.
(3)当t为何值时,以B,P,Q三点为顶点的三角形是等腰三角形?
(4)是否存在时刻t,使得PQ⊥BD?若存在,求出t的值;若不存在,请说明理由.
(本题满分11分)
如图(1),已知正方形ABCD在直线MN的上方,BC在直线MN上,E是BC上一点,以AE为边在直线MN的上方作正方形AEFG.(1)连接GD,求证:△ADG≌△ABE;(2分)
(2)连接FC,观察并猜测∠FCN的度数,并说明理由;(3分)
(3)如图(2),将图(1)中正方形ABCD改为矩形ABCD,AB=a,BC=b(a、b为常数),E是线段BC上一动点(不含端点B、C),以AE为边在直线MN的上方作矩形AEFG,使顶点G恰好落在射线CD上.判断当点E由B向C运动时,∠FCN的大小是否总保持不变,若∠FCN的大小不变,请用含a、b的代数式表示tan∠FCN的值;若∠FCN的大小发生改变,请举例说明.(4分)

如图所示,菱形ABCD的顶点A、B在x轴上,点A在点B的左侧,点D在y轴的正半轴上,∠BAD=60°,点A的坐标为(-2,0).
⑴求线段AD所在直线的函数表达式.
⑵动点P从点A出发,以每秒2个单位长度的速度,按照A→D→C→B的顺序在菱形的边上匀速运动,设运动时间为t秒.求t为何值时,以点P为圆心、以1为半径的圆与对角线AC相切?
在一次远足活动中,某班学生分成两组,第一组由甲地匀速步行到乙地后原路返回,第二组由甲地匀速步行经乙地继续前行到丙地后原路返回,两组同时出发,设步行的时间为t(h),两组离乙地的距离分别为S1(km)和S2(km),图中的折线分别表示S1、S2与t之间的函数关系.
 (1)甲、乙两地之间的距离为 km,乙、丙两地之间的距离为 km;
(1)甲、乙两地之间的距离为 km,乙、丙两地之间的距离为 km; (2)求第二组由甲地出发首次到达乙地及由乙地到达丙地所用的时间分别是多少?
(2)求第二组由甲地出发首次到达乙地及由乙地到达丙地所用的时间分别是多少?(3)求图中线段AB所表示的S2与t间的函数关系式,并写出自变量t的取值范围.
如图,在平面直角坐标系中,△ ABC的三个顶点的坐标分别为A(0,1),B(-1,1),C(-1,3)。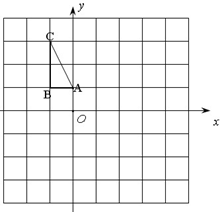
(1)画出△ABC关于x轴对称的△A1B1C1,并写出点C1的坐标;
(2)画出△ABC绕原点O顺时针方向旋转90°后得到的△A2B2C2,并写出点C2的坐标;,
(3)将△A2B2C2平移得到△ A3B3C3,使点A2的对应点是A3,点B2的对应点是B3,点C2的对应点是C3(4,-1),在坐标系中画出△ A3B3C3,并写出点A3,B3的坐标。