已知一次函数的图象与反比例函数的图象交于点A(3,2)、B(-2, m).求这两个函数的关系式,并在同一坐标系(如图7)中画出这两个函数的图象;
观察(1)中两个函数的图象,写出使一次函数的值大于反比例函数的值时,自变量x的取值范围.

如图,在△ABC中,AB=AC,AD和BE是高,它们相交于点H,且AE=BE
求证:AH=2BD 
如图,△ACD和△BCE都是等腰直角三角形,∠ACD=∠BCE=90°,AE交DC于F,BD分别交CE,AE于点G、H试猜测线段AE和BD数量关系,并说明理由
如图,∠B=∠E=Rt∠,AB=AE,∠1=∠2,请证明∠3=∠4
如图,在△ABC中,AB=AC,∠ABC=72°.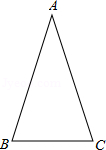
(1)用直尺和圆规作∠ABC的平分线BD交AC于点D(保留作图痕迹,不要求写作法);
(2)在(1)中作出∠ABC的平分线BD后,求∠BDC的度数.
如图所示,在平面直角坐标系中,M是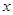 轴正半轴上一点,⊙M与
轴正半轴上一点,⊙M与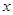 轴的正半轴交于A、B两点,A在B的左侧,且OA、OB的长是方程
轴的正半轴交于A、B两点,A在B的左侧,且OA、OB的长是方程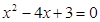 的两根,ON是⊙M的切线,N为切点,N在第四象限.
的两根,ON是⊙M的切线,N为切点,N在第四象限.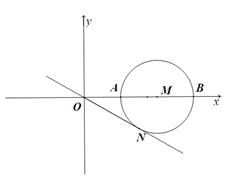
(1)求⊙M的直径;
(2)求直线ON的函数关系式;
(3)在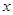 轴上是否存在一点T,使△OTN是等腰三角形?若存在,求出T的坐标;若不存在,请说明理由.
轴上是否存在一点T,使△OTN是等腰三角形?若存在,求出T的坐标;若不存在,请说明理由.