为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
| 性别 是否需要志愿者 |
男 |
女 |
| 需要 |
40 |
30 |
| 不需要 |
160 |
270 |
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
(3)根据(2)的结论,能否提出更好的调查方法来估计该地区的老年人中需要志愿者提供帮助的老年人的比例?说明理由.
(本小题满分13分)已知椭圆的顶点与双曲线 的焦点重合,它们的离心率之和为
的焦点重合,它们的离心率之和为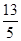 ,若椭圆的焦点在
,若椭圆的焦点在 轴上,求椭圆的方程.
轴上,求椭圆的方程.
(本小题满分13分)已知圆 与直线
与直线 相交于
相交于 两点.
两点.
(1)求弦 的长;
的长;
(2)若圆 经过
经过 ,且圆
,且圆 与圆
与圆 的公共弦平行于直线
的公共弦平行于直线 ,求圆
,求圆 的方程.
的方程.
(本题满分13分)已知抛物线 过点
过点 。
。
(1)求抛物线 的标准方程,并求其准线方程;
的标准方程,并求其准线方程;
(2)是否存在平行于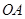 (
( 为坐标原点)的直线
为坐标原点)的直线 ,使得直线
,使得直线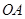 与
与 的距离等于
的距离等于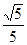 ?
?
若存在,求直线 的方程,若不存在,说明理由。
的方程,若不存在,说明理由。
(3)过抛物线 的焦点
的焦点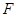 作两条斜率存在且互相垂直的直线
作两条斜率存在且互相垂直的直线 ,设
,设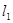 与抛物线
与抛物线 相交于点
相交于点 ,
, 与抛物线
与抛物线 相交于点
相交于点 ,求
,求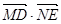 的最小值。
的最小值。
(本题满分13分)如图,在四棱锥 中,底面
中,底面 是矩形,知
是矩形,知
 。
。
(1)证明: ;
;
(2)求异面直线 与
与 所成的角的余弦值;
所成的角的余弦值;
(3)求二面角 的大小余弦值。
的大小余弦值。
(本题满分13分)已知三点
(1)求以 为焦点且过点
为焦点且过点 的椭圆的标准方程;
的椭圆的标准方程;
(2)设点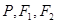 关于直线
关于直线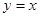 的对称点分别为
的对称点分别为 ,求以
,求以 为焦点且过点
为焦点且过点 的双曲线的标准方程。
的双曲线的标准方程。