(本题满分13分)已知抛物线 过点
过点 。
。
(1)求抛物线 的标准方程,并求其准线方程;
的标准方程,并求其准线方程;
(2)是否存在平行于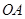 (
( 为坐标原点)的直线
为坐标原点)的直线 ,使得直线
,使得直线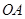 与
与 的距离等于
的距离等于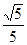 ?
?
若存在,求直线 的方程,若不存在,说明理由。
的方程,若不存在,说明理由。
(3)过抛物线 的焦点
的焦点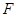 作两条斜率存在且互相垂直的直线
作两条斜率存在且互相垂直的直线 ,设
,设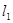 与抛物线
与抛物线 相交于点
相交于点 ,
, 与抛物线
与抛物线 相交于点
相交于点 ,求
,求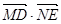 的最小值。
的最小值。
定义 数列 对 , 满足:
① ;
② ;
③ .
(1) 对前 4 项 的数列, 可以是 数列吗? 说明理由.
(2) 若 是 数列, 求 的值.
(3) 是否存在 , 使得存在 数列 , 对任意 , 满足 ? 若存在, 求出所有这样的 ; 若不存在, 请说明理由.
已知椭圆 过点 , 以四个顶点围成的四边形面积为 .
(1) 求椭圆 的标准方程.
(2) 过点 的直线 的斜率为 , 交椭圆 于不同的两点 , 直线 交 于点 , 若 , 求 的取值范围.
已知函数 .
(1) 若 , 求 在 处的切线方程.
(2) 若函数 在 处取得极值, 求 的单调区间, 以及最大值和最小值.
为加快新冠肺炎检测效率,某检测机构采取“ 合 1 检测法", 即将 个人的拭自样本合并检测, 若为阴性, 则可确定有样本都是阴性的; 若为阳性, 则还需要对本组的每个人再做检测. 现有 100 人, 已知其中 2 人 感染病毒.
(1) ①若采用“ 10 合 1 检测法”, 且两名感染患者在同一组, 求总检测次数.
② 已知 10 人分成一组, 分 10 组, 两名感染患者在同一组的概率为 , 定义随机变量 为总检测次数, 求检测次数 的分布列和数学期望 .
(2) 若采用“ 5 合 1 检测法”, 检测次数 的期望为 , 试比较 与 的大小(直接写出结果).
已知正方体 , 点 为 中点, 直线 交平面 于点 .

(1) 求证:点 为 中点.
(2) 若点 为棱 上一点, 且二面角 的余弦值为 , 求 .