为加快新冠肺炎检测效率,某检测机构采取“ 合 1 检测法", 即将 个人的拭自样本合并检测, 若为阴性, 则可确定有样本都是阴性的; 若为阳性, 则还需要对本组的每个人再做检测. 现有 100 人, 已知其中 2 人 感染病毒.
(1) ①若采用“ 10 合 1 检测法”, 且两名感染患者在同一组, 求总检测次数.
② 已知 10 人分成一组, 分 10 组, 两名感染患者在同一组的概率为 , 定义随机变量 为总检测次数, 求检测次数 的分布列和数学期望 .
(2) 若采用“ 5 合 1 检测法”, 检测次数 的期望为 , 试比较 与 的大小(直接写出结果).
先后随机投掷2枚正方体骰子,其中 表示第
表示第 枚骰子出现的点数,
枚骰子出现的点数, 表示第
表示第 枚骰子出现的点数.
枚骰子出现的点数.
(Ⅰ)求点 在直线
在直线 上的概率;
上的概率;
(Ⅱ)求点 满足
满足 的概率.
的概率.
已知函数
(1)用五点法画出它在一个周期内的闭区间上的图象;
(2)求函数 的单调增区间;
的单调增区间;
(3)若 ,求
,求 的最大值和最小值.
的最大值和最小值.
已知函数
(Ⅰ)若 是从
是从 三个数中任取的一个数,
三个数中任取的一个数, 是从
是从 四个数中任取的一个数,求
四个数中任取的一个数,求 为偶函数的概率;
为偶函数的概率;
(Ⅱ)若 ,
, 是从区间
是从区间 任取的一个数,求方程
任取的一个数,求方程 有实根的概率.
有实根的概率.
已知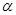 为第三象限角,
为第三象限角, .
.
(1)化简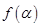 (2)若
(2)若 ,求
,求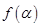 的值
的值
已知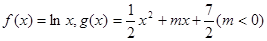 ,直线
,直线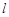 与函数
与函数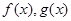 的图像都相切,且与函数
的图像都相切,且与函数 的图像的切点的横坐标为1.
的图像的切点的横坐标为1.
(1)求直线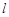 的方程及
的方程及 的值;
的值;
(2)若 (其中
(其中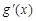 是
是 的导函数),求函数
的导函数),求函数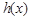 的最大值;
的最大值;
(3)当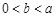 时,求证:
时,求证: .
.