设椭圆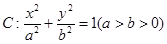 的左、右焦点分别为
的左、右焦点分别为 ,上顶点为
,上顶点为 ,在
,在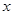 轴负半轴上有一点
轴负半轴上有一点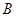 ,满足
,满足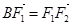 ,且
,且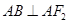 .
.
(Ⅰ)求椭圆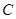 的离心率;
的离心率;
(Ⅱ)D是过 三点的圆上的点,D到直线
三点的圆上的点,D到直线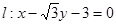 的最大距离等于椭圆长轴的长,求椭圆
的最大距离等于椭圆长轴的长,求椭圆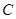 的方程;
的方程;
(Ⅲ)在(2)的条件下,过右焦点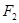 作斜率为
作斜率为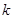 的直线
的直线 与椭圆
与椭圆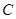 交于
交于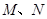 两点,在
两点,在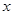 轴上是否存在点
轴上是否存在点 使得以
使得以 为邻边的平行四边形是菱形,如果存在,求出
为邻边的平行四边形是菱形,如果存在,求出 的取值范围,如果不存在,说明理由.
的取值范围,如果不存在,说明理由.
(本小题满分12分)设等差数列{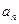 }的前n项和为
}的前n项和为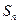 ,且
,且 。
。
(1)求数列{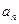 }的通项公式及前n项和公式;
}的通项公式及前n项和公式;
(2)设数列{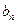 }的通项公式为
}的通项公式为 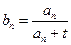 ,是否存在正整数t,使得
,是否存在正整数t,使得 成等差数列?若存在,求出t和m的值;若不存在,请说明理由
成等差数列?若存在,求出t和m的值;若不存在,请说明理由
(本小题满分12分)设数列{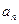 }满足
}满足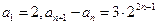 。
。
(1)求数列{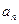 }的通项公式;
}的通项公式;
(2)令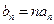 ,求数列{
,求数列{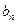 }的前n项和
}的前n项和 。
。
(本小题满分12分)某工厂要建造一个长方体形无盖贮水池,其容积为4800m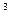 , 深为3 m。如果池底每平方米的造价为150元,池壁每平方米的造价为120元,怎样设计水池能使总造价最低?最低总造价是多少?
, 深为3 m。如果池底每平方米的造价为150元,池壁每平方米的造价为120元,怎样设计水池能使总造价最低?最低总造价是多少?
(本小题满分12分)已知等差数列{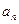 }的前n项和为
}的前n项和为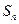 ,且
,且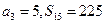 。
。
(1)求数列{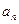 }的通项公式;
}的通项公式;
(2)设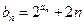 ,求数列{
,求数列{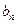 }的前n项和
}的前n项和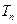 。
。
(本小题满分10分)已知函数f (x)="2" asin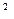 x+2 sinx cosx-a的图象过点(0,
x+2 sinx cosx-a的图象过点(0,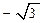 )。
)。
(1)求常数a
(2)当x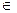 [0,
[0, ] 时,求函数f (x) 的值域
] 时,求函数f (x) 的值域