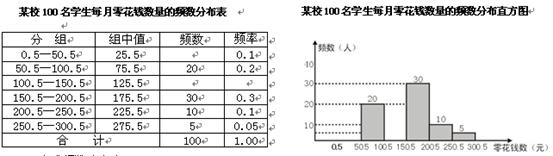
未成年人思想道德建设越来越受到社会的关注．某青少年研究机构随机调查了某校100学生每月花零花钱的数量（钱数取整数元），以便引导学生树立正确的消费观，根据调查数据制成了如下的频数分布表（部分空格未填），并绘制成下面的频数分布直方图．请你思考并回答下列问题：完成频数分布表；
补全频数分布直方图；
研究认为应对消费200元以上的学生提出勤俭节约的建议，试估计应对该校1800名学生中约有多少名学生提出该项建议？
如图：已知A（-4，n）、B（2，-4）是一次函数y1=kx+b的图象与反比例函数y2=
的图象
的两个交点．
（1）求反比例函数和一次函数的解折式．
（2）求直线AB与x轴的交点C的坐标及△AOB的面积．
（3）求不等式y1<y2
的解集（请直接写出答案）．
如图，抛物线y=﹣（x﹣1）2+c与x轴交于A，B（A，B分别在y轴的左右两侧）两点，与y轴的正半轴交于点C，顶点为D，已知A（﹣1，0）．
（1）求点B，C的坐标；
（2）将△COB沿x轴向右平移t个单位长度（0＜t＜3）得到△QPE．△QPE与△CDB重叠部分（如图中阴影部分）面积为S，求S与t的函数关系式，并写出自变量t的取值范围．
某商店欲购进甲、乙两种商品，已知甲的进价是乙的进价的一半，进3件甲商品和1件乙商品恰好用200元．甲、乙两种商品的售价每件分别为80元、130元，该商店决定用不少于6710元且不超过6810元购进这两种商品共100件．
（1）求这两种商品的进价．
（2）该商店有几种进货方案？哪种进货方案可获得最大利润，最大利润是多少？
如图，已知AB是⊙O的直径，点C、D在⊙O上，点E在⊙O外，∠EAC=∠D=60°．
（1）求证：AE是⊙O的切线
（2）当BC=4时，求劣弧AC的长
如图，已知
，
是一次函数
的图象和反比例函数
的图象的两个交点．
（1）求反比例函数和一次函数的解析式；
（2）求△
的面积；