“五·一”假期,某单位组织部分员工到 、
、 、
、 三地旅游,单位购买前往各地的车票种类、数量绘制成如图所示的条形统计图.根据统计图回答下列问题:
三地旅游,单位购买前往各地的车票种类、数量绘制成如图所示的条形统计图.根据统计图回答下列问题:
前往
 地的车票有_____张,前往
地的车票有_____张,前往 地的车票占全部车票的________
地的车票占全部车票的________ ;
;若单位决定采用随机抽取的方式把车票分配给
 名员工,在看不到车票的条件下,每人抽取一张(所有车票的形状、大小、质地完全相同且充分洗匀),那么员工小王抽到去
名员工,在看不到车票的条件下,每人抽取一张(所有车票的形状、大小、质地完全相同且充分洗匀),那么员工小王抽到去 地车票的概率为______;
地车票的概率为______;若最后剩下一张车票时,员工小张、小李都想要,决定采用抛掷一枚各面分别标有数字
 ,
, ,
, ,
, 的正四面体骰子的方法来确定,具体规则是:每人各抛掷一次,小张掷得着地一面的数字比小李掷得着地一面的数字大,车票给小张,否则给小李. 试用列表法或画树状图的方法分析,这个规则对双方是否公平?
的正四面体骰子的方法来确定,具体规则是:每人各抛掷一次,小张掷得着地一面的数字比小李掷得着地一面的数字大,车票给小张,否则给小李. 试用列表法或画树状图的方法分析,这个规则对双方是否公平?
计算:
在平面直角坐标系中,抛物线y=ax2+bx+2的图象过 和
和 ,与
,与 轴交于点
轴交于点 ,与
,与 轴交于另一点
轴交于另一点 ,点
,点 是原点
是原点 关于点
关于点 的对称点,连结
的对称点,连结 、
、 ,设点
,设点 。
。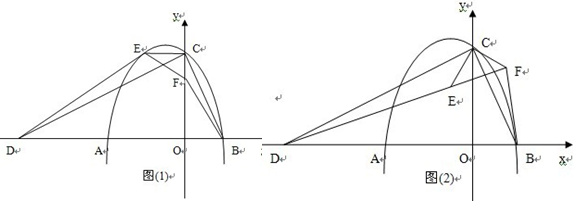
(1)求抛物线的解析式;
(2)连结 、
、 ,①求
,①求 的值;②将
的值;②将 绕点
绕点 旋转,在旋转过程中如图(2),线段
旋转,在旋转过程中如图(2),线段 和
和 的比值会变吗?请说明理由;
的比值会变吗?请说明理由;
(3)设点 是直线
是直线 上方的抛物线上一点,连结
上方的抛物线上一点,连结 ,以
,以 为边作图示一侧的正方形,随着点
为边作图示一侧的正方形,随着点 的运动,正方形的大小,位置也随之改变,当顶点
的运动,正方形的大小,位置也随之改变,当顶点 或
或 恰好落在
恰好落在 轴上时,直接写出对应点
轴上时,直接写出对应点 的坐标。
的坐标。
为了绿化城市,美化环境,园林部门计划购买甲、乙两种树苗共800株,甲种树苗每株24元,乙种树苗每株30元,相关资料表明:甲、乙两种树苗的成活率分别为85%,90%。
(1)若购买这两种树苗共用去21000元,则甲、乙两种树苗各购买多少株?
(2)若要使这批树苗的总成活率不低于88%,则甲种树苗至多购买多少株?
(3)在(2)的条件下,应如何选购树苗,使购买树苗的费用最低?并求出最低费用。
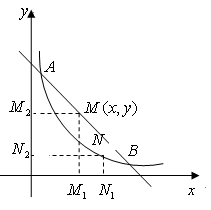
如图,已知一次函数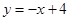 的图象与反比例函数
的图象与反比例函数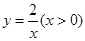 的图象分别交于
的图象分别交于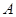 ,
,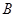 两点,点
两点,点 是一次函数图象在第一象限部分上的任意一点,过
是一次函数图象在第一象限部分上的任意一点,过 分别向
分别向 轴,
轴,  轴作垂线,垂足分别为
轴作垂线,垂足分别为 ,
, ,设矩形
,设矩形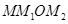 的面积为
的面积为 ,点
,点 为反比例函数图象上任意一点,过
为反比例函数图象上任意一点,过 分别向
分别向 轴,
轴, 轴作垂线,垂足分别为
轴作垂线,垂足分别为 ,
, ,设矩形
,设矩形 的面积为
的面积为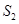 。
。 
(1)若设点 的坐标为
的坐标为 ,请写出
,请写出 关于
关于 的函数关系式,并求
的函数关系式,并求 的最大值.
的最大值.
(2)观察图形,通过确定的取值范围,比较 ,
,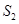 的大小
的大小
联合国规定每年的月日是“世界环境日”,为配合今年的“世界环境日”宣传活动,某校课外活动小组对全校师生开展了以“爱护环境,从我做起”为主题的问卷调查活动,将调查结果分析整理后制成了下面的两个统计图.其中:
| A.能将垃圾放到规定的地方,而且还会对垃圾分类。 | B.能将垃圾放到规定地方,但不会考虑垃圾分类。 | C.偶尔会将垃圾放到规定的地方。 | D.随手乱扔垃圾。 根据以上信息回答下列问题: |

(1)该校课外活动小组共调查了多少人?并补全上面的条形统计图;
(2)如果该校共有师生2400人,那么随手乱扔垃圾的约有多少人?