如图抛物线过坐标原点O和x轴上另一点E,顶点M为 (2,4);矩形ABCD顶点A与点O重合,AD、AB分别在x轴、y轴上,且AD=2,AB=3. 求该抛物线所对应的函数关系式;
将矩形ABCD以每秒1个单位长度的速从图示位置沿x轴正方向匀速平行移动,同时一动点P也以相同速度从点A出发向B匀速移动,设它们运动时间为t秒(0≤t≤3),直线AB与该抛物线交点为N
①当t=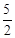 时,判断点P是否在直线ME上,说明理由;
时,判断点P是否在直线ME上,说明理由;
②设以P、N、C、D为顶点的多边形面积为S,试问S是否存在最大值?说明理由.
化简求值: ,其中
,其中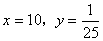
计算与化简:(1)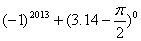
(2)20122-2011×2013
(3)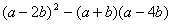
如图,抛物线y=-x2+mx+n与x轴分别交于点A(4,0),B(-2,0),与y轴交于点C.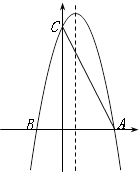
(1)求该抛物线的解析式;
(2)M为第一象限内抛物线上一动点,点M在何处时,△ACM的面积最大;
(3)在抛物线的对称轴上是否存在这样的点P,使得△PAC为直角三角形?若存在,请求出所有可能点P的坐标;若不存在,请说明理由.
如图,平面直角坐标系中,直线y=-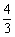 x+8分别交x轴、y轴于点B、点A,点D从点A出发沿射线AB方向以每秒1个单位长的速度匀速运动,同时点E从点B出发沿射线BC方向以每秒
x+8分别交x轴、y轴于点B、点A,点D从点A出发沿射线AB方向以每秒1个单位长的速度匀速运动,同时点E从点B出发沿射线BC方向以每秒 个单位长的速度匀速运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥AO于点F,连接DE、EF.
个单位长的速度匀速运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥AO于点F,连接DE、EF.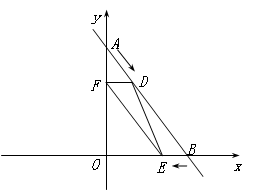
(1)当t为何值时,△BDE与△BAO相似;
(2)写出以点D、F、E、O为顶点的四边形面积s与运动时间t之间的函数关系;
(3)是否存在这样一个时刻,此时以点D、F、E、B为顶点的四边形是菱形,如果存在,求出相应的t的值;如果不存在,请说明理由.
如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,连接DH交AC于点O.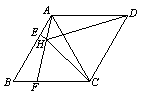
(1)△ABF≌△CAE;
(2)HD平分∠AHC吗?为什么?