设数列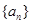 的前n项和为
的前n项和为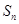 ,点
,点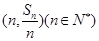 均在函数y=-x+12的图像上.
均在函数y=-x+12的图像上.
(Ⅰ)写出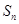 关于n的函数表达式;
关于n的函数表达式;
(Ⅱ)求证:数列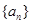 是等差数列;
是等差数列;
(Ⅲ)求数列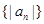 的前n项的和.
的前n项的和.
已知椭圆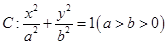 的离心率
的离心率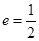 ,点A为椭圆上一点,
,点A为椭圆上一点, .
.
(1)求椭圆C的方程;
(2)设动直线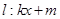 与椭圆C有且只有一个公共点P,且与直线
与椭圆C有且只有一个公共点P,且与直线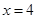 相交于点Q.问:在
相交于点Q.问:在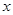 轴上是否存在定点M,使得以PQ为直径的圆恒过定点M?若存在,求出点M的坐标;若不存在,说明理由.
轴上是否存在定点M,使得以PQ为直径的圆恒过定点M?若存在,求出点M的坐标;若不存在,说明理由.
设 .
.
(1)求函数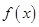 的图象在点
的图象在点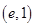 处的切线方程;
处的切线方程;
(2)求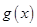 的单调区间;
的单调区间;
(3)当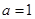 时,求实数
时,求实数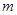 的取值范围,使得
的取值范围,使得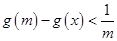 对任意
对任意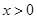 恒成立.
恒成立.
已知数列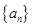 中,
中,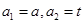 (常数
(常数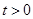 ),
),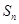 是其前
是其前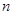 项和,且
项和,且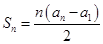 .
.
(1)试确定数列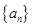 是否为等差数列,若是,求出其通项公式;若不是,说明理由;
是否为等差数列,若是,求出其通项公式;若不是,说明理由;
(2)令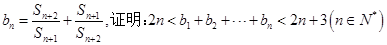 .
.
如图所示,四边形ABCD是边长为2的正方形,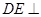 平面ABCD,AF//DE,DE=2AF,BE与平面ABCD所成角的正切值为
平面ABCD,AF//DE,DE=2AF,BE与平面ABCD所成角的正切值为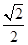 .
.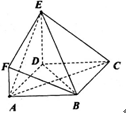
(1)求证:AC//平面EFB;
(2)求二面角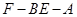 的大小.
的大小.
2015年元旦联欢晚会某师生一块做游戏,数学老师制作了六张卡片放在盒子里,卡片上分别写着六个函数:分别写着六个函数: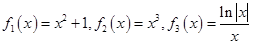 ,
,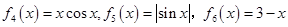 .
.
(1)现在取两张卡片,记事件A为“所得两个函数的奇偶性相同”,求事件A的概率;
(2)从盒中不放回逐一抽取卡片,若取到一张卡片上的函数是奇函数则停止抽取,否则继续进行,记停止时抽取次数为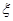 ,写出
,写出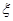 的分布列,并求其数学期望.
的分布列,并求其数学期望.