如图1,在直角梯形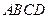 中,
中,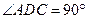 ,
,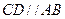 ,
,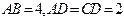 ,
,  为线段
为线段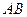 的中点.将
的中点.将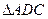 沿
沿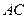 折起,使平面
折起,使平面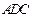
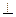 平面
平面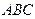 ,得到几何体
,得到几何体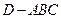 ,如图2所示.
,如图2所示.
(Ⅰ) 求证: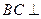 平面
平面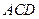 ;
;
(Ⅱ) 求二面角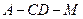 的余弦值.
的余弦值.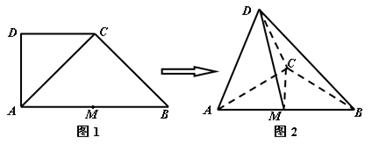
某项竞赛分别为初赛、复赛、决赛三个阶段进行,每个阶段选手要回答一个问题.规定
正确回答问题者进入下一阶段竞赛,否则即遭淘汰.已知某选手通过初赛、复赛、决赛的概率分别是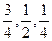 ,且各阶段通过与否相互独立.
,且各阶段通过与否相互独立.
(I)求该选手在复赛阶段被淘汰的概率;
(II)设该选手在竞赛中回答问题的个数为 ,求
,求 的分布列、数学期望和方差.
的分布列、数学期望和方差.
设集合 .
.
(Ⅰ)求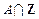 ;
;
(Ⅱ)若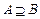 ,求
,求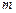 的取值范围.
的取值范围.
在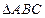 中,
中,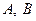 为锐角,角
为锐角,角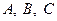 所对的边分别为
所对的边分别为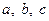 ,且
,且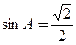 ,
,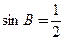 .
.
(Ⅰ)求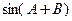 的值;
的值;
(Ⅱ)若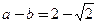 ,求
,求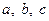 的值.
的值.
在平面直角坐标系中,O为坐标原点,已知两点M(1,—3)、N(5,1),若动点C满足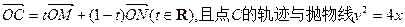 交于A、B两点。
交于A、B两点。
(I)求证: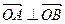 ;
;
(2)在x轴上是否存在一点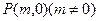 ,使得过点P的直线l交抛物线
,使得过点P的直线l交抛物线 于D、E两点,并以线段DE为直径的圆都过原点。若存在,请求出m的值,若不存在,请说明理由。
于D、E两点,并以线段DE为直径的圆都过原点。若存在,请求出m的值,若不存在,请说明理由。