在△ABC中,设A、B、C的对边分别为a、b、c,向量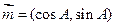 ,
,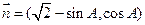 且
且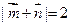 .
.
(Ⅰ)求角A的大小;
(Ⅱ)若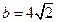 ,
, ,求△ABC的面积.
,求△ABC的面积.
(本小题满分12分)
已知定义在正实数集上的函数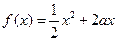 ,
, ,其中
,其中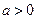 .设两曲线
.设两曲线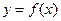 ,
, 有公共点,且在该点处的切线相同.
有公共点,且在该点处的切线相同.
(1)用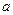 表示
表示 ,并求
,并求 的最大值;
的最大值;
(2)求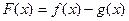 的极值.
的极值.
(本小题满分12分)
已知函数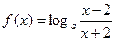 的定义域为[
的定义域为[ ,
, ],值域为
],值域为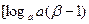 ,
, ,并且
,并且 在
在 ,
,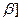 上为减函数.
上为减函数.
(1)求a的取值范围;
(2)求证: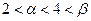 ;
;
(3)求函数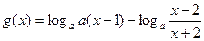 在区间
在区间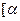 ,
,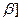 的最大值M.
的最大值M.
(本小题满分12分)
设函数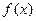 的定义域为
的定义域为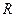 ,对任意
,对任意 有
有 ,且
,且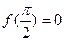 ,
,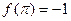 .
.
(1)求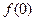 的值;
的值;
(2)求证: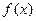 是偶函数,且
是偶函数,且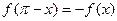 ;
;
(3)若 时,
时, ,求证:
,求证: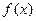 在
在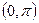 上单调递减.
上单调递减.
(本小题满分12分)
二次函数 ,
,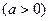 ,设
,设 的两个实根为
的两个实根为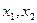 ,
,
(1)如果 且
且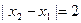 ,求
,求 的值;
的值;
(2)如果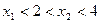 ,设函数
,设函数 的对称轴为
的对称轴为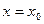 ,求证:
,求证: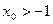 .
.