现对某市工薪阶层关于“楼市限购政策”的态度进行调查，随机抽查了50人，他们月收入（单位：百元）的频数分布及对“楼市限购政策”赞成人数如下表：

月收入（单位百元）	[15,25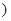	[25，35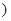	[35，45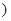	[45，55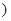	[55，65	[65,75
频数	5	10	15	10	5	5
赞成人数	4	8	12	5	2	1

 
（Ⅰ）根据以上统计数据填写下面2×2列联表，并回答是否有99%的把握认为月收入以5500元为分界点对“楼市限购政策” 的态度有差异？

	月收入不低于55百元的人数	月收入低于55百元的人数	合计
赞成
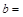不赞成
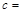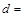合计

 
（Ⅱ)若从月收入在[55，65）的被调查对象中随机选取两人进行调查，求至少有一人不赞成“楼市限购政策”的概率.
（参考公式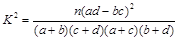：，其中.）
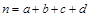参考值表：

P()	0.50	0.40	0.25	0.15	0.10	0.05	0.025	0.010	0.005	0.001
	0.455	0.708	1.323	2.072	2.706	3.841	5.024	6.635	7.879	10.828

科目 数学   题型 解答题   难度 中等