已知椭圆 的离心率为
的离心率为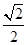 ,其左、右焦点分别为
,其左、右焦点分别为 ,点
,点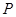 是椭圆上一点,且
是椭圆上一点,且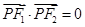 ,
,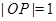 (
( 为坐标原点).
为坐标原点).
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)过点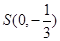 且斜率为
且斜率为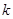 的动直线
的动直线 交椭圆于
交椭圆于 两点,在
两点,在 轴上是否存在定点
轴上是否存在定点 ,使以
,使以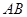 为直径的圆恒过这个点?若存在,求出
为直径的圆恒过这个点?若存在,求出 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
已知平面上的动点P(x,y)及两个定点A(-2,0),B(2,0),直线PA,PB的斜率分别为K1,K2且K1K2=-
(1).求动点P的轨迹C方程;
(2).设直线L:y=kx+m与曲线C交于不同两点,M,N,当OM⊥ON时,求O点到直线L的距离(O为坐标原点)
如图,E是以AB为直径的半圆弧上异于A,B的点,矩形ABCD所在平面垂直于该半圆所在的平面,且AB=2AD=2。
(1).求证:EA⊥EC;
(2).设平面ECD与半圆弧的另一个交点为F。
①求证:EF//AB;
②若EF=1,求三棱锥E—ADF的体积
已知向量 ,设函数
,设函数 .
.
(1).求函数f(x)的最小正周期;
(2).已知a,b,c分别为三角形ABC的内角对应的三边长,A为锐角,a=1, ,且
,且 恰是函数f(x)在
恰是函数f(x)在 上的最大值,求A,b和三角形ABC的面积.
上的最大值,求A,b和三角形ABC的面积.
设数列 是等差数列,且
是等差数列,且 且
且 成等比数列。
成等比数列。
(1).求数列 的通项公式
的通项公式
(2).设 ,求前n项和
,求前n项和 .
.
已知f(x)=|x+1|+|x-1|,不等式f(x)的解集为M.
(1)求M;
(2)当a,b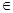 M时,证明:2|a+b|<|4+ab|.
M时,证明:2|a+b|<|4+ab|.