已知在数列{an}中，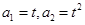
（t>0且t≠1）．
是函数
的一个极值点．
（1）证明数列
是等比数列，并求数列
的通项公式；
（2）记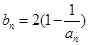
，当t=2时，数列
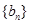的前n项和为Sn，求使Sn>2012的n的最小值；
（3）当t=2时，是否存在指数函数g（x），使得对于任意的正整数n有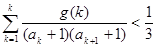
成立？若存在，求出满足条件的一个g（x）；若不存在，请说明理由．
（本小题满分15分）（文）如图，在四棱锥P-ABCD中，底面为直角梯形，AD//BC，
BAD=
，PA⊥底面ABCD，且PA=AD=AB=2BC，M、N分别为PC、PB的中点.
（Ⅰ）求证：PB⊥DM；
（Ⅱ） 求CD与平面ADMN所成角的余弦
（本小题满分14分）
已知函数
其中实数
。
（1）若a=-2，求曲线
在点
处的切线方程；
（2）若
在x=1处取得极值，试讨论的单调性。
（本小题满分12分） 已知函数
，若
，试确定函数
的单调区间；
（本小题满分12分）
已知函数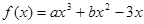
在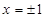
处取得极值.
（1）求f(x)的解析式
（2）求f(x)的单调区间
．（本小题满分12分）
已知向量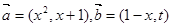
，若函数
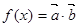在区间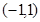
上是增函数，求
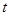的取值范围。