.(本小题满分12分)
已知向量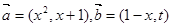 ,若函数
,若函数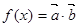 在区间
在区间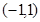 上是增函数,求
上是增函数,求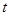 的取值范围。
的取值范围。
在等差数列 中,已知
中,已知 ,求首项
,求首项 与公差d
与公差d
数列 中,已知
中,已知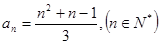 。
。
(1)写出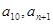 ;(2)
;(2) 是否是数列中的项?如果是,是第几项?
是否是数列中的项?如果是,是第几项?
一个人在建筑物的正西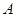 点,测得建筑物顶的仰角是
点,测得建筑物顶的仰角是 ,这个人再从
,这个人再从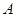 点向南走到
点向南走到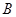 点,再测得建筑物顶的仰角是
点,再测得建筑物顶的仰角是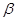 ,设
,设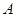 ,
,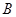 间的距离是
间的距离是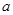 .
.
证明:建筑物的高是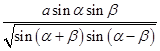 .
.
飞机的航线和山顶在同一个铅垂平面内,已知飞机的高度为海拔20250m,速度为1000km/h,飞行员先看到山顶的俯角为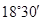 ,经过150s后又看到山顶的俯角为
,经过150s后又看到山顶的俯角为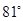 ,求山顶的海拔高度(精确到1m).
,求山顶的海拔高度(精确到1m).
一架飞以326km/h的速度,沿北偏东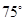 的航向从城市A出发向城市B飞行,18min以后,飞机由于天气原因按命令改飞另一个城市C,问收到命令时飞机应该沿什么航向飞行,此时离城市C的距离是多少?
的航向从城市A出发向城市B飞行,18min以后,飞机由于天气原因按命令改飞另一个城市C,问收到命令时飞机应该沿什么航向飞行,此时离城市C的距离是多少?