(本小题满分12分)
为了让学生更多地了解“数学史”知识,某中学高二年级举办了一次“追寻先哲的足迹,倾听数学的声音”的数学史知识竞赛活动,共有 名学生参加了这次竞赛。为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为
名学生参加了这次竞赛。为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为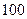 分)进行统计。请你根据下面的频率分布表,解答下列问题:
分)进行统计。请你根据下面的频率分布表,解答下列问题:
| 序号 (  ) ) |
分组 (分数) |
本组中间值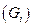 |
频数 (人数) |
频率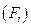 |
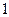 |
 |
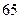 |
①[] |
 |
 |
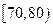 |
 |
 |
②] |
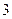 |
 |
 |
③ |
 |
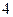 |
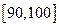 |
 |
④ |
⑤ |
| 合 计 |
 |
  |
(1)填充频率分布表中的空格(在解答中直接写出对应空格序号的答案);
(2)为鼓励更多的学生了解“数学史”知识,成绩不低于 分的同学能获奖,请估计在参赛的
分的同学能获奖,请估计在参赛的 名学生中大概有多少同学获奖?
名学生中大概有多少同学获奖?
|
(3)请根据频率分布表估计该校高二年级参赛的800名同学的平均成绩。
(本小题满分13分)
某初级中学共有学生2000名,各年级男、女生人数如下表:
| 初一年级 |
初二年级 |
初三年级 |
|
| 女生 |
373 |
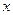 |
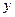 |
| 男生 |
377 |
370 |
 |
已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19.
(1)求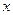 的值;
的值;
(2)现用分层抽样的方法在全校抽取48名学生,问应在初三年级抽取多少名?
(3)已知 ,
, ,求初三年级中女生比男生多的概率.
,求初三年级中女生比男生多的概率.
(本小题满分13分)
已知函数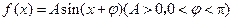 ,
,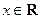 的最大值是1,其图像经过点
的最大值是1,其图像经过点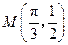 .
.
(1)求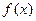 的解析式;
的解析式;
(2)已知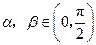 ,且
,且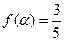 ,
,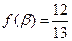 ,求
,求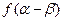 的值.
的值.
已知
的角
所对的边分别是
,设向量
.
(1)若
,求证:
为等腰三角形;
(2)若
,边长
,角
,求
的面积.
已知
是公差为
的等差数列,
是公比为
的等比数列.
(1)若
,是否存在
,有
说明理由;
(2)找出所有数列
和
,使对一切
,
,并说明理由;
(3)若
试确定所有的
,使数列
中存在某个连续
项的和是数列
中的一项,请证明.
已知函数
的反函数.定义:若对给定的实数
,函数
与
互为反函数,则称
满足"
和性质";若函数
与
互为反函数,则称
满足"
积性质".
(1)判断函数
是否满足"1和性质",并说明理由;
(2)求所有满足"2和性质"的一次函数;
(3)设函数
对任何
,满足"
积性质".求
的表达式.