浙江理）已知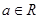
，函数
（1）求曲线
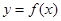在点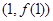
处的切线方程；
（2）当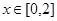
时，求
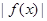的最大值.
参加市数学调研抽测的某校高三学生成绩分析的茎叶图和频率分布直方图均受到不同程度的破坏，但可见部分信息如下，据此解答如下问题：
（1）求参加数学抽测的人数
、抽测成绩的中位数及分数分别在
，
内的人数；
（2）若从分数在
内的学生中任选两人进行调研谈话，求恰好有一人分数在内的概率．
在如图所示的几何体中，四边形
是矩形，
平面
，
，
∥
，
，
，
分别是
，
的中点．
（1）求证：
∥平面；
（2）求证：
平面
．
已知向量
，
，函数
，
三个内角
的对边分别为
.
（1）求
的单调递增区间；
（2）若
，求
的面积
．
已知函数
．
（1）设
是函数
的极值点，求
的值并讨论的单调性；
（2）当
时，证明：＞
．
已知椭圆
：
（
）的焦距为
，且过点（
，
），右焦点为
．设
，
是上的两个动点，线段
的中点
的横坐标为
，线段的中垂线交椭圆于
，
两点．
（1）求椭圆的方程；
（2）求
的取值范围．